Andrew NG Coursera 课程编程作业

发表于 | 更新于 | 分类于

使用课程推荐的Octave进行编程实现，可以将Octave理解为开源版本的MATLAB

Ex1: Linear Regression

  1. 读入数据

    1
    2
    3
    4
    5
    6
    data = load('ex1data1.txt'); % 导入的数据文件为用逗号隔开的两列，第一列为x，第二列为y
    X = data(:, 1);
    y = data(:, 2);
    % 可以尝试绘图
    % figure;plot(x,y);
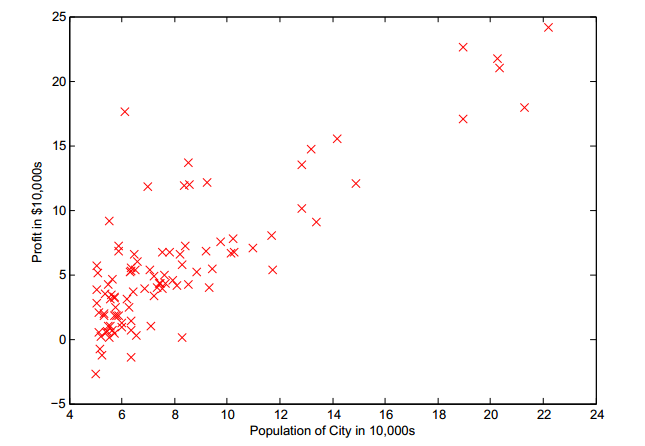
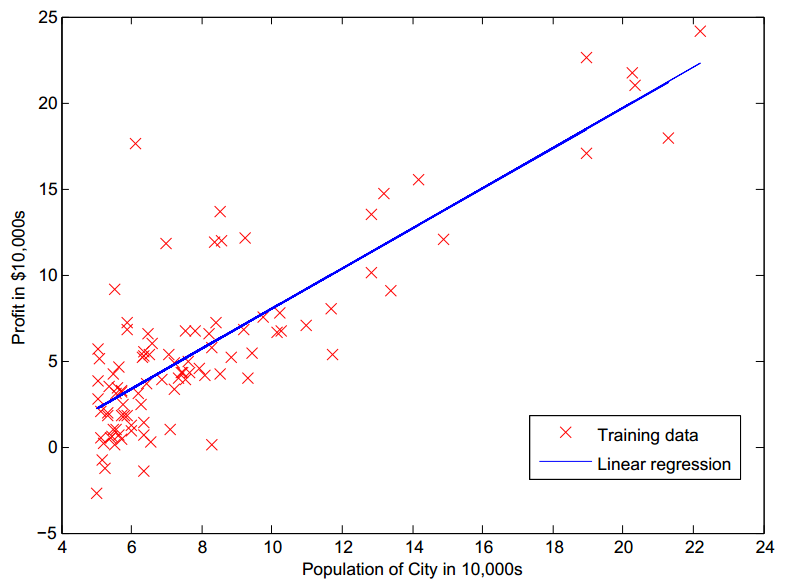
    m = length(y);

    数据分布图如下：

  2. 梯度下降前的数据预处理与设置

    1
    2
    3
    4
    5
    6
    X = [ones(m,1),data(:,1)]; % 添加x0列，都设为1
    theta = zeros(2,1); % 初始化θ值

    % 梯度下降的一些设置信息
    iterations = 1500; % 迭代次数
    alpha = 0.01; % 学习率α

  3. 计算损失函数

    线性回归的损失函数为：

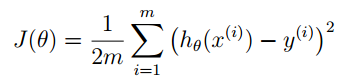
    1
    2
    3
    4
    5
    6
    7
    % 定义一个函数computeCost来计算损失函数
    function J = computeCost(X, y, theta)
    	m = length(y);
    	predictions = X*theta; % 计算预测值hθ
    	sqerrors = (predictions - y).^2; % 计算平方误，矩阵的点乘运算得到的是一个向量
    	J = 1/(2*m)* sum(sqerrors);
    end

  4. 执行梯度下降

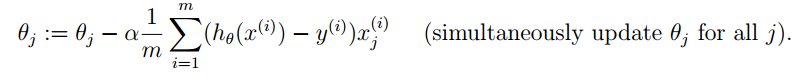
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    % 定义一个函数gradientDescent来执行梯度下降，为了后面观察梯度下降过程中损失函数的变化，记录每一步迭代后的损失函数值
    function [theta, J_history] = gradientDescent(X, y, theta, alpha, iterations)
    	m = length(y);
    	J_history = zeros(num_iters, 1);
    	% 以迭代次数为唯一迭代终止条件
    	for iter = 1:num_iters
    		% 计算梯度
    		predictions = X*theta;
    		updates = X'*(predictions - y);
    		theta = theta - alpha*(1/m)*updates;
    		J_history(iter) = computeCost(X, y, theta);
    	end
    end

  5. 绘制拟合直线

    1
    2
    3
    hold on; % 保留之前的绘图窗口，在这个绘图窗口继续画出拟合直线
    plot(X(:,2), X*theta, '-');
    legend('Training data', 'Linear regression');

Ex2: Logistic回归

目标：

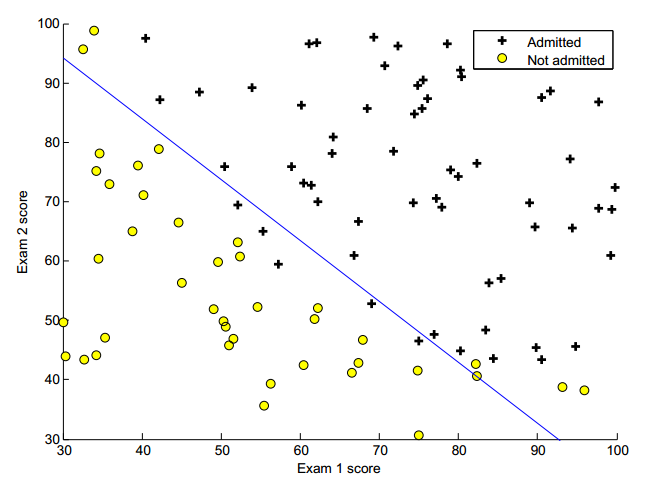
构建一个logistics回归模型，依据学生两次考试的成绩来预测一个学生能否被大学录取

通过的输入数据文件为ex2data1.txt：

1
2
3
4
5
6
7
8
9
10
11
12
# 为用逗号隔开的3列，分别为：exam1Score,exam2Score,lable

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
...

  1. 读入数据，并画出数据分布散点图

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    data = load('ex2data1.txt');
    x = data(:,:2);
    y = data(:,3);

    % 画图
    %% 区分出两类样本
    pos = find(y==1);
    neg = find(y==0);
    figure;
    %% 画出pos类样本
    plot(x(pos,1), x(pos,2),'k+','MarkerSize', 3);
    hold on;
    %% 画出neg类样本
    plot(x(neg,1), x(neg,2),'ko','MarkerSize', 3);
    xlab('Exam 1 score');
    ylab('Exam 2 score');
    legend('Admitted', 'Not admitted');
    hold off;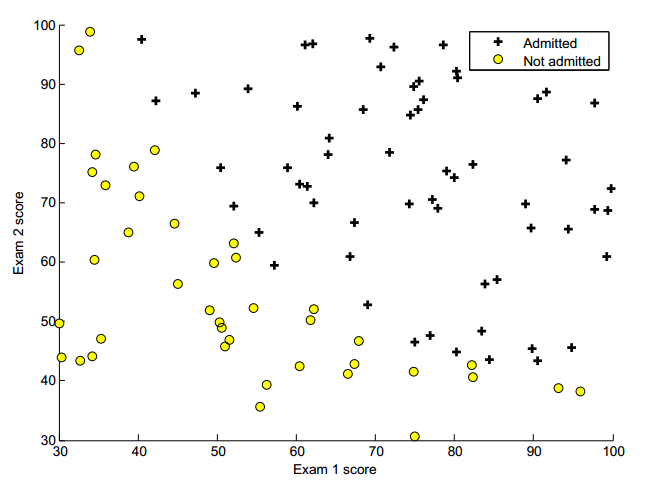

    要得到的目标函数为 sigmoid 函数：

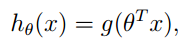
  2. 计算Cost和gradient

    1
    2
    3
    4
    5
    6
    7
    8
    [m,n] = size(x);
    X = [ones(m),data(:,:2)];
    initialTheta = zeros(1,n+1);
    % 计算初始的Cost和gradient
    [initalCost,initialGradient] = costFunction(X,y,initialTheta);
    % 打印出初始时的Cost和gradient
    fprintf('Cost at initial theta(zeros): %f\n",initialCost);
    fprintf('Gradient at initial theta(zeros): %f\n",initialGradient);

    在计算初始的Cost (initalCost) 和 gradient (initialGradient) 时，调用了自定义的函数costFunction

    损失函数为：

    梯度的计算公式为：

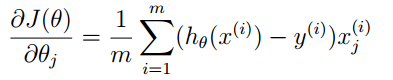
    下面给出costFunction函数的定义：

    1
    2
    3
    4
    5
    6
    7
    function [jVal,gradient] = costFunction(x,y,theta)
    	predict = sigmoid(x*theta);
    	leftCost = -y'*log(predict);
    	rightCost = -(1-y)'*log(1-predict);
    	jVal = (1/m)*(leftCost+rightCost);
    	gradient = (1/m)*((predict-y)'*x);
    end

    在上面的costFunction函数中又调用了sigmoid函数，定义为：

    1
    2
    3
    function g = sigmoid(x)
    	g = 1./(1+exp(-x));
    end

  3. 优化目标函数

    使其目标函数的Cost最小化，即

    可以像练习一那样使用传统的梯度下降方法进行参数的优化，但Octave内部自带了fminunc函数，可以用于非约束优化问题（unconstrained optimization problem）的求解

    fminunc函数的用法为：

    1
    2
    3
    4
    5
    6
    7
    %% 设置fminunc函数的内部选项
    options = optmset('GradObj', 'on', 'MaxIter', 400);
    % 'GradObj', 'on' 设置梯度目标参数为打开状态，即需要给这个算法提供一个梯度
    % 'MaxIter', 400 设置最大迭代次数

    %% 使用fminunc函数执行非约束优化
    [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

    一般情况下costFunction函数和它的函数名一样，只计算Cost值，不过由于这里要用到fminunc这个非约束优化函数，该函数需要提供Cost和gradient，所以在前面costFunction函数时，增加了一个计算梯度值的功能

  4. 画出决策分界面 (Decision Boundary)

    先像前面的第一步那样，画出原始数据分布散点图

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    % 画图
    %% 区分出两类样本
    pos = find(y==1);
    neg = find(y==0);
    figure;
    %% 画出pos类样本
    plot(x(pos,1), x(pos,2),'k+','MarkerSize', 3);
    %% 画出neg类样本
    plot(x(neg,1), x(neg,2),'ko','MarkerSize', 3);
    xlab('Exam 1 score');
    ylab('Exam 2 score');

    然后在散点图的基础上，把分界线画出来

    分界线满足：

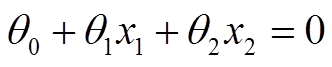
    得到x1和x2直接的关系为：

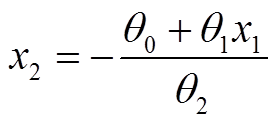
    1
    2
    3
    4
    5
    6
    7
    hold on;
    % 只需要选择两个点即可将直线画出
    plot_x = [min(X(:,2))-2, max(X(:,2))+2];
    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
    plot(plot_x, plot_y)
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    hold off;