从CONCOCT入手理解宏基因组binning

1. 宏基因组binning简介

Metagenome 组装完成后，我们得到的是成千上万的 contigs，我们需要知道哪些 contigs 来自哪一个基因组，或者都有哪些微生物的基因组。所以需要将 contigs 按照物种水平进行分组归类，称为 “bining”

Supervised binning methods: use databases of already sequenced genomes to label contigs into taxonomic classes

Unsupervised (clustering) methods: look for natural groups in the data

Both supervised and unsupervised methods have two main elements: a metric to define the similarity between a given contig and
a bin, and an algorithm to convert those similarities into assignments

一个很容易想到的策略就是，将组装得到的片段与已知物种的参考基因组进行比对，根据同源性进行归类。然而目前大多数的微生物的基因组还没有测序出来，因此限制了这种方法的可行性。

目前主流的 bining 策略利用的是 contigs 的序列组成特点。

2. binning原理

2.1. 可用于binning的特征

根据核酸组成信息来进行binning：k-mer frequencies

依据：来自同一菌株的序列，其核酸组成是相似的

例如根据核酸使用频率（oligonucleotide frequency variations），通常是四核苷酸频率（tetranucleotide frequency），GC含量和必需的单拷贝基因等

优势：即便只有一个样品的宏基因组数据也可以进行binning，这在原理上是可操作的

不足：由于很多微生物种内各基因型之间的基因组相似性很高，想利用1个样品的宏基因组数据通过核酸组成信息进行binning，效果往往并不理想或难度很大。利用核酸组成信息进行binning，基本上只适合那些群落中物种基因型有明显核酸组成差异的，例如低GC含量和一致的寡核苷酸使用频率
根据丰度信息来进行binning

依据：来自同一个菌株的基因在不同的样品中 ( 不同时间或不同病理程度 ) 的丰度分布模式是相似的【PMID: 24997787】。

原因：比如，某一细菌中有两个基因，A和B，它们在该细菌基因组中的拷贝数比例为 A:B = 2:1，则不管在哪个样品中这种细菌的数量有多少，这两个基因的丰度比例总是为 2:1

优势：这种方法更有普适性，一般效果也比较好，能达到菌株的水平

不足：必须要大样本量，一般至少要50个样本以上，至少要有2个组能呈现丰度变化 ( 即不同的处理，不同的时间，疾病和健康，或者不同的采样地点等 ) ，每个组内的生物学重复也要尽量的多

对于像质粒这样的可移动遗传单元 (mobile genetic elements (MGEs))，由于其复制独立于细菌染色体，则同一种细菌的不同个体，该质粒的拷贝数可能存在差异，使得无法用丰度信息进行有效地bining
同时依据核酸组成和丰度变化信息

将核酸组成信息和丰度差异信息创建一个综合的距离矩阵，既能保证binning效果，也能相对节约计算资源，现在比较主流的binning软件多是同时依据核酸组成和丰度变化信息
根据基因组甲基化模式

依据：不同的细菌，其基因组甲基化模式不同，平均一种细菌有3种特意的甲基化 motif。MGEs (mobile genetic elements) 中含有 MTase 基因，其基因水平转移是细菌甲基化组多样性的驱动因素。虽然 MGEs 在不同个体的拷贝数不同，但是都存在，因此具有相同 MGEs 的细菌个体，其总遗传物质（包括染色体和 MGEs ）都会受到相同的MTase的作用而得到相同的甲基化模式。

2.2. 从哪些序列下手进行binning？

从原始的clean reads，还是从组装成的contig，还是从预测到的gene，都可以。根据基于聚类的序列类型的不同，暂且分为reads binning， contig binning和 genes binning

比较这三种binning的优劣：

contig binning

由于核酸组成和物种丰度变化模式在越长的序列中越显著和稳定，基于contig binning效果可能更好

reads binning

基于reads binning的优势是可以聚类出宏基因组中丰度非常低的物种

考虑到在宏基因组组装中reads利用率很低，单样品5Gb测序量情况下，环境样品组装reads利用率一般只有10%左右，肠道样品或极端环境样品组装reads利用率一般能达到30%，这样很多物种，尤其是低丰度的物种可能没有被组装出来，没有体现在gene 或者contig 中，因此基于reads binning 才有可能得到低丰度的物种

如 Brian Cleary 等 (DOI:10.1038/nbt.3329.Detection) 利用基于 reads binning 的 latent strain analysis 可以聚类出丰度低至0.00001%的菌株。此方法虽然得到更全面的 bins，但低丰度 bins 信息依旧不完整。

genes binning

应用非常广泛

原因可能是（1）基于genes丰度变化模式进行binning可操作性比较强，宏基因组分析中肯定都会计算gene丰度，一般不会计算contig丰度，gene丰度数据可以信手拈来；（2）基于genes binning有很多可参考的文献，过程也并不复杂，可复制性强；（3）对计算机资源消耗比较低

总体来说应用最广泛的就是基于genes binning 和 contig binning

Naseer Sangwan 等 (DOI: 10.1186/s40168-016-0154-5) 总结了 contig binning 的算法和软件（如下表）

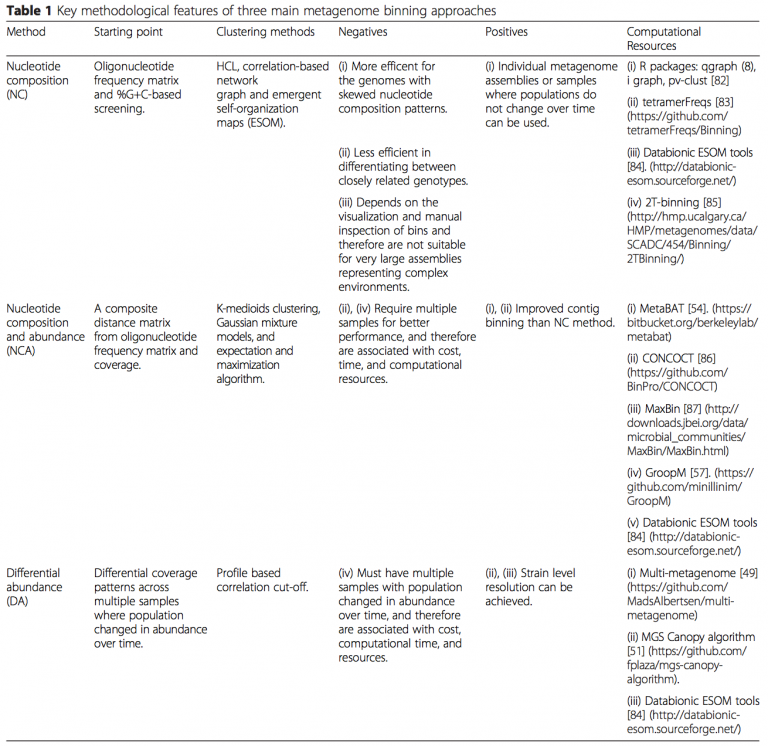
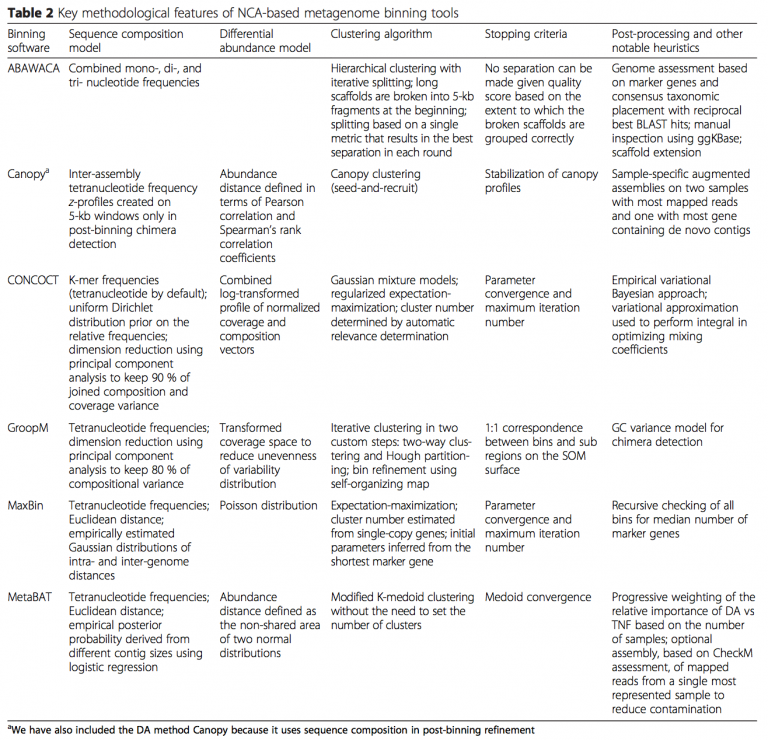
基于Genes abundance binning的一般流程

在宏基因组做完组装和基因预测之后，把所有样品中预测到的基因混合在一起，去冗余得到unique genes集合，对这个unique genes集合进行binning，主要是根据gene在各个样品中的丰度变化模式，计算gene之间的相关性，利用这种相关性进行聚类

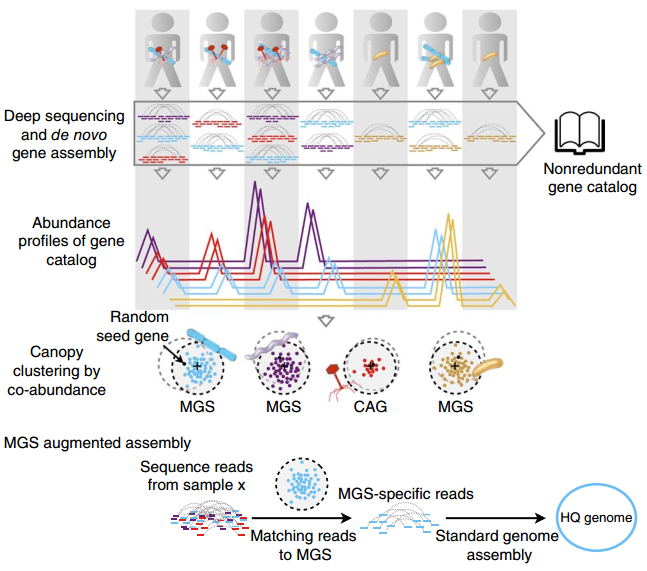
该图中的聚类过程类似于K-means聚类：随机选择几个seed genes作为诱饵，计算其他基因丰度分布模式与seed genes的相关性，按照固定的相关性值PCC>0.9，将它们归属于不同seed genes所代表的类，然后在聚好的类内重新选择seed genes，进行迭代，最终聚类得到一个个基因集合，较大的集合（超过700个基因）称为 metagenomic species (MGS)，较小的集合称为 co-abundance gene group (CAG)

基于 binning 结果进行单菌组装：

Sequence reads from individual samples that map to the MGS genes and their contigs are then extracted and used to assembly a draft genome sequence for an MGS

3. 详述CONCOCT的binning原理

结合序列组成特征 (sequence composition) 和跨样本覆盖度特征 (coverage across multiple samples) 进行binning

在进行binning之前需要将所有样本的reads进行混拼 (coassembly) 得到contigs

Sequence composition features

以 k-mer 长度等于5为例

将相互之间成反向互补关系的 5-mers pairs 记做一种，则总共有512种 5-mers，对每一条contig计算其各自 5-mers 的组成频率从而构造出一个长度为v=512的向量 Z_i：

Z_i = (Z_i,1, …, Z_i,v)

为了保证每个 5-mers 频率的计数非零（为后面的对数转换做准备），进行伪计数处理，然后用该序列的 5-mers的总数进行标准化，得到新的向量 Z_i^‘：
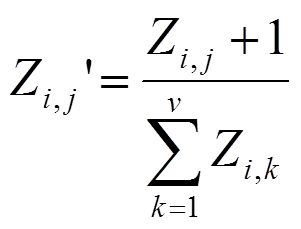
Contig coverage features

用段序列比对软件，将各个样本（总共有M个样本）的reads比对到contigs上，计算每条contigs在每个样本中的 coverage (Mapped reads * read length / contig length)，得到表示 congtig i 的 coverage 的向量 Y_i：

Y_i = (Y_i,1, …, Y_i,M)

两轮标准化处理：

伪计数处理：额外添加一条比对到该 contig 上的 read；再用该样本内所有 contigs（contigs总数为N）的 coverage 进行标准化，得到新的向量 Y_i^‘：

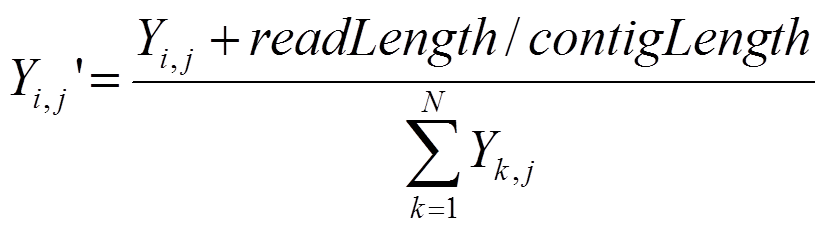
然后再在contig内部进行标准化，得到新的向量 Y_i^‘’：
Combine two features

将表示某一个 contig i 的序列组成特征的向量 Z_i^‘ 和 coverage 特征向量 Y_i^‘’合并成组成一个新的特征向量 X_i（向量长度为E=V+M），同时进行对数转换：

X_i = { log(Z_i^‘) , log(Y_i^‘’) }
PCA降维，保留能解释至少90%的方差的主成分（共保留前D个主成分，D < E）

矩阵维数变化：N x E => N x D
cluster contigs into bins

使用高斯混合模型 (Gaussian mixture model)

基于高斯混合模型(GMM)的期望最大化（EM）聚类：
可以把高斯混合模型简单理解为k-means算法的概率统计版本
- 回顾k-means聚类
  
  k-means聚类有这样一个数据分布的假设：属于同一簇的数据样本聚集成近乎于圆形的团
  
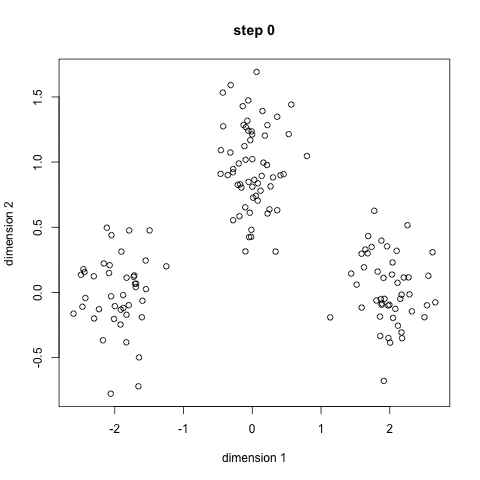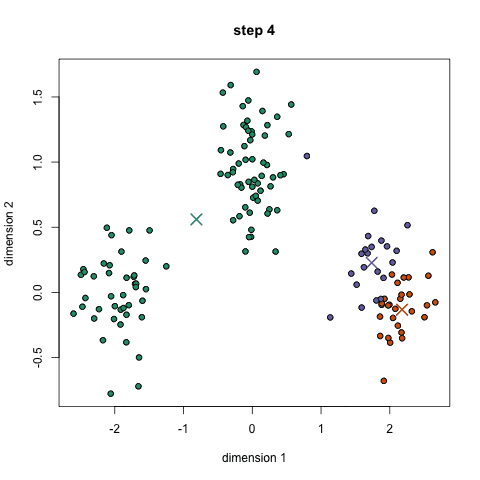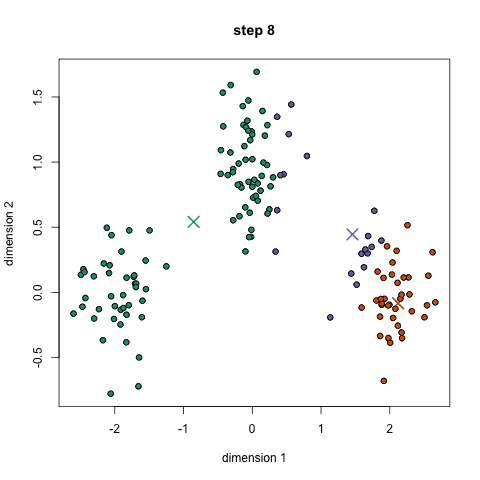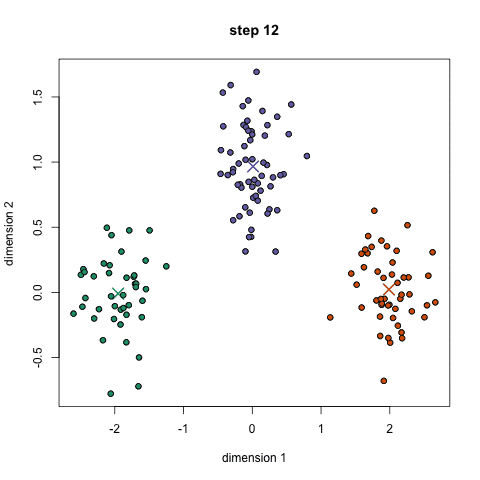
  k-means的优点是速度非常快，因为我们真正要做的就是计算点和组中心之间的距离；计算量少！因此，它具有线性复杂性o（n）
  
  另一方面，k-means有两个缺点。首先，您必须先确定聚类的簇数量。理想情况下，对于一个聚类算法，我们希望它能帮我们解决这些问题，因为它的目的是从数据中获得一些洞察力。k-均值也从随机选择聚类中心开始，因此它可能在算法的不同运行中产生不同的聚类结果。因此，结果可能不可重复，缺乏一致性。
- GMM算法
  
  k-means的一个主要缺点是它简单地使用了集群中心的平均值，对于以圆形方式聚集成簇的数据，k-means算法的聚类效果很好，但是当簇不是圆形时，k均值会失效，这也是将均值用作簇中心的后果
  
  通过下面的图片，我们可以看到为什么这不是最好的方式
  
  在左手边，人眼可以很明显地看到，有两个半径不同的圆形星团以相同的平均值为中心。k-means不能处理这个问题，因为不同簇的平均值非常接近
  
  高斯混合模型（gmms）具有比K-means更好的灵活性。使用GMMs，其基于的数据分布的假设为数据点是高斯分布，可以简单理解为属于同一簇的数据样本聚集成近乎于环状或椭圆形的团，相对于环形或椭圆形的数据而言，这个假设的严格程度与均值相比弱很多
  
  那高斯混合模型是如何实现聚类的呢？
  
  与k-means算法类似，首先需要知道数据需要聚成k个簇，然后随机初始化k个簇各种所对应的高斯分布的两个参数：均值μ与方差σ，然后基于EM算法从数据中学到各个簇最佳的参数：C₁ ~ N(μ₁, σ₁²), C₂ ~ N(μ₂, σ₂²) … C_k ~ N(μ_k, σ_k²)
  
  接着就可以基于上一步学习到的参数对每个数据点划分簇的归属了，比如对于样本i，其簇的归属为：

4. 拆解CONCOCT的流程

4.1. Assembling Metagenomic Reads

# 将多个样本的测序数据fastq文件，按照双端分别进行合并
$ cat $CONCOCT_TEST/reads/Sample*_R1.fa > All_R1.fa
$ cat $CONCOCT_TEST/reads/Sample*_R2.fa > All_R2.fa

# 拼接
$ velveth velveth_k71 71 -fasta -shortPaired -separate All_R1.fa All_R2.fa
$ velvetg velveth_k71 -ins_length 400 -exp_cov auto -cov_cutoff auto

velveth:

takes in a number of sequence files, produces a hashtable, then outputs two files in an output directory (creating it if necessary), Sequences and Roadmaps, which are necessary to velvetg.

语法：
1
2
> ./velveth output_directory hash_length [[-file_format][-read_type] filename]
>

velvetg:

Velvetg is the core of Velvet where the de Bruijn graph is built then manipulated

4.2. Cutting up contigs

将大片段的contigs (>=20kb)，切成一个个10kb的小片段，当切到尾部只剩不到20kb时，停止切割，以防切得过碎

1	python $CONCOCT/scripts/cut_up_fasta.py -c 10000 -o 0 -m contigs/velvet_71.fa > contigs/velvet_71_c10K.fa

4.3. Map, Remove Duplicate and Quant Coverage

使用 Bowtie2 执行 mapping 操作
用 MarkDuplicates（Picard中的一个工具）去除 PCR duplicates
用 BEDTools genomeCoverageBed 基于 mapping 得到的 bam 文件计算每个contigs的coverage

（1） Map, Remove Duplicate

其中1、2步操作可以由CONCOCT中提供的脚本map-bowtie2-markduplicates.sh完成

先要自行建好这些contigs的bowtie2索引

1 2	# index for contigs $ bowtie2-build contigs/velvet_71_c10K.fa contigs/velvet_71_c10K.fa

用map-bowtie2-markduplicates.sh脚本完成 mapping -> remove duplicate

for f in $CONCOCT_TEST/reads/*_R1.fa; do
    mkdir -p map/$(basename $f);
    cd map/$(basename $f);
    bash $CONCOCT/scripts/map-bowtie2-markduplicates.sh -ct 1 -p '-f' $f $(echo $f | sed s/R1/R2/) pair $CONCOCT_EXAMPLE/contigs/velvet_71_c10K.fa asm bowtie2;
    cd ../..;
done

-c option to compute coverage histogram with genomeCoverageBed

-t option is number of threads

-p option is the extra parameters given to bowtie2. In this case -f

-k 保留中间文件

随后的5个参数：

pair1, the fasta/fastq file with the #1 mates

pair2, the fasta/fastq file with the #2 mates

pair_name, a name for the pair used to prefix output files

assembly, a fasta file of the assembly to map the pairs to

assembly_name, a name for the assembly, used to postfix outputfiles

outputfolder, the output files will end up in this folder

如果要自己逐步执行第1、2两步，则可以通过以下方式实现：

# Index reference, Burrows-Wheeler Transform
$ bowtie2-build SampleA.fasta SampleA.fasta

# Align Paired end, sort and index
bowtie2 \
	-p 32 \
	-x SampleA.fasta \
	-1 $Data/SampleA.1.fastq \
	-2 $Data/SampleA.2.fastq | \
	samtools sort -@ 18 -O BAM -o SampleA.sort.bam
samtools index SampleA.sort.bam

# Mark duplicates and index
java -Xms32g -Xmx32g -XX:ParallelGCThreads=15 -XX:MaxPermSize=2g -XX:+CMSClassUnloadingEnabled \
    -jar picard.jar MarkDuplicates \
    I=./SampleA.sort.bam \
    O=./SampleA.sort.md.bam \
    M=./SampleA.smd.metrics \
    VALIDATION_STRINGENCY=LENIENT \
    MAX_FILE_HANDLES_FOR_READ_ENDS_MAP=1000 \
    REMOVE_DUPLICATES=TRUE # 该参数默认为false，即在输出中不过滤duplicate，但是会对这些记录的flag进行修改标记
samtools index ./SampleA.sort.md.bam

（2）Quant Coverage

第3步，计算每个contigs的coverage，用gen_input_table.py脚本

# usage: gen_input_table.py [-h] [--samplenames SAMPLENAMES] [--isbedfiles] fastafile bamfiles [bamfiles ...]
# --samplenames 写有样品名的文件，每个文件名一行
# --isbedfiles  如果在上一步map时运行了genomeCoverageBed，则可以加上此参数后直接用 *smds.coverage文件。如果没运行genomeCoverageBed，则不加此参数，依旧使用bam文件。

$ python $CONCOCT/scripts/gen_input_table.py --isbedfiles \
	--samplenames <(for s in Sample*; do echo $s | cut -d'_' -f1; done) \
	../contigs/velvet_71_c10K.fa */bowtie2/asm_pair-smds.coverage \
	> concoct_inputtable.tsv

注：

这个脚本可以接受两种类型的输入

（1）对bamfiles执行genomeCoverageBed (bedtools genomecov得到的*smds.coverage文件，此时要使用--isbedfiles参数，这样脚本只执行下面提到的第2步操作——计算每条contig的平均depth（又称为这条contig的abundance）；

（2）原始的bamfiles，则脚本要执行下面提到的两步操作；

也可以自己写命令逐步实现，这样有利于加深对工具的理解

计算每条contig的depth分布（histograms）

1	$ bedtools genomecov -ibam ./SampleA.smds.bam > ./SampleA.smds.coverage

bedtools genomecov默认计算histograms，如输出为chr1 0 980 1000，则说明在contig chr1上depth=0的碱基数为980bp，该contig长度为1000bp

例如：

> $ cat A.bed
> chr1  10  20
> chr1  20  30
> chr2  0   500
> 
> $ cat my.genome
> chr1  1000
> chr2  500
> 
> $ bedtools genomecov -i A.bed -g my.genome
> chr1   0  980  1000  0.98
> chr1   1  20   1000  0.02
> chr2   1  500  500   1
> genome 0  980  1500  0.653333
> genome 1  520  1500  0.346667
>

输出格式为：

chromosome

depth of coverage from features in input file

number of bases on chromosome (or genome) with depth equal to column 2

size of chromosome (or entire genome) in base pairs

size of chromosome (or entire genome) in base pairs

计算每条contig的平均depth

有两种计算方法：

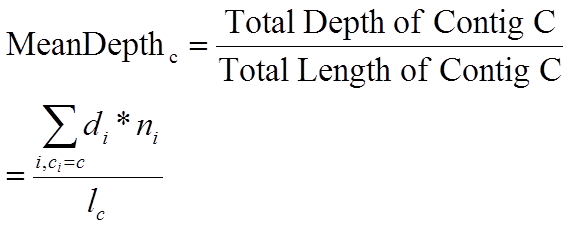
或

第二种计算方法本质上就是加权平均

awk 'BEGIN {pc=""} 
{
    c=$1;
    if (c == pc) {
        cov=cov+$2*$5;
    } else {
      print pc,cov;
      cov=$2*$5;
    pc=c}
} END {print pc,cov}' SampleA.smds.coverage | tail -n +2 > SampleA.smds.coverage.percontig

（3）Generate linkage table

接着要构建 linkage per sample between contigs，目前不是很理解它这一步的目的

尝试作简单的理解：

# usage: bam_to_linkage.py [-h] [--samplenames SAMPLENAMES] [--regionlength REGIONLENGTH] [--fullsearch] [-m MAX_N_CORES] [--readlength READLENGTH] [--mincontiglength MINCONTIGLENGTH] fastafile bamfiles [bamfiles ...]
# --samplenames 写有样品名的文件，每个文件名一行
# --regionlength contig序列中用于linkage的两端长度 [默认 500]
# --fullsearch 在全部contig中搜索用于linkage
# -m 最大线程数，每个ban文件对应一个线程
# --readlength untrimmed reads长度 [默认 100]
# --mincontiglength 识别的最小contig长度 [默认 0]

cd $CONCOCT_EXAMPLE/map
python bam_to_linkage.py -m 8 --regionlength 500 --fullsearch --samplenames sample.txt $DATA/SampleA.fasta ./SampleA.smds.bam > SampleA_concoct_linkage.tsv
mv SampleA_concoct_linkage.tsv ../concoct-input

# 输出文件格式
# 共2+6*i列 (i样品数)，依次为contig1、contig2、nr_links_inward_n、nr_links_outward_n、nr_links_inline_n、nr_links_inward_or_outward_n、read_count_contig1_n、read_count_contig2_n
# where n represents sample name. 
# Links只输出一次，如 contig1contig2 输出，则 contig2contig1 不输出

# contig1: Contig linking with contig2
# contig2: Contig linking with contig1
# nr_links_inward: Number of pairs confirming an inward orientation of the contigs -><-
# nr_links_outward: Number of pairs confirming an outward orientation of the contigs <--> 
# nr_links_inline: Number of pairs confirming an outward orientation of the contigs ->->
# nr_links_inward_or_outward: Number of pairs confirming an inward or outward orientation of the contigs. This can be the case if the contig is very short and the search region on both tips of a contig overlaps or the --fullsearch parameter is used and one of the reads in the pair is outside
# read_count_contig1/2: Number of reads on contig1 or contig2. With --fullsearch read count over the entire contig is used, otherwise only the number of reads in the tips are counted.

参考资料：

(1) Quince C, Walker A W, Simpson J T, et al. Shotgun metagenomics, from sampling to analysis[J]. Nature Biotechnology, 2017, 35(9):833.

(2) Nielsen H B, Almeida M, Juncker A S, et al. Identification and assembly of genomes and genetic elements in complex metagenomic samples without using reference genomes[J]. Nature Biotechnology, 2014, 32(8):822-828.

(3) Sangwan N, Xia F, Gilbert J A. Recovering complete and draft population genomes from metagenome datasets[J]. Microbiome, 2016, 4(1):8.

(4) Abubucker, S. et al. Metabolic reconstruction for metagenomic data and its application to the human microbiome. PLoS Comput. Biol. 8, e1002358(2012).

(5) Beaulaurier J, Zhu S, Deikus G, et al. Metagenomic binning and association of plasmids with bacterial host genomes using DNA methylation.[J]. Nature Biotechnology, 2017, 36(1).

(6) Alneberg, J. et al. Binning metagenomic contigs by coverage and composition. Nat. Methods 11, 1144–1146 (2014).

(7) CONCOCT’s documentation

(8) Manual for Velvet

(9) BEDtools官网

(10) 【Yue Zheng博客】宏基因组binning-CONCOCT

(11) AI研习社《数据科学中必须熟知的5种聚类算法》