最近在给面临中考的表妹补课,补的是数学和物理(化学尝试过,表示hold不住),补课会遇到了一些还挺有意思,稍有难度的题,就把它们的解题过程记录了下来
人到油腻中年,只能拿这样的东西练练脑子了,主要为了防止老年痴呆
Week-1
题目是这样的:
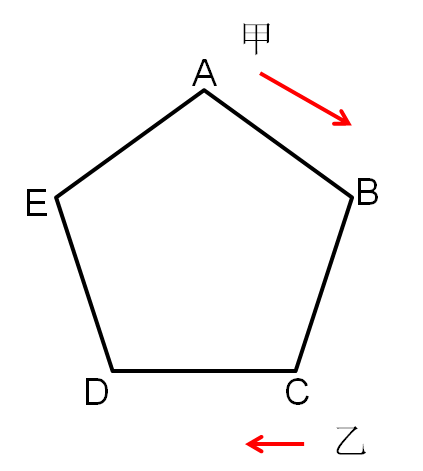
正五边形广场ABCDE的边长为80m,甲、乙两个同学做游戏,分别从A、C两点处同时出发,沿A-B-C-D-E-A的方向绕广场行走,甲的速度为50m/min,乙的速度为46m/min,则两人第一次刚走到同一条边上时,( )
A. 甲在顶点A处
B. 甲在顶点B处
C. 甲在顶点C处
D. 甲在顶点D处
求解思路:
这本质上是一个同向同时的追击问题
想象一下,甲追上乙即两者相遇时的场景,两人第一次刚走到同一条边上的场景肯定发生在两者相遇之前,也就是说题目要求的那个时刻那个场景是发生在追击过程中的
可以很容易地想到,两人第一次刚走到同一条边上时,落在后面的甲肯定刚好落在这个五边形的某一个顶点上,这意味着甲此时刚好完整地走完了x条边,则此时甲移动的路程为80x
由于此时,乙与甲在同一条边上,则可设此时甲乙之间的距离为k,则此时乙移动的路程为80x+k-160
考虑到甲乙是同时运动的,它们的运动时间总是相同的,则
$$
\frac{80x}{50}=\frac{80x+k-160}{46}
$$
根据这个公式,可以推出K的表达式为:
$$k=ax+b$$
a和b分别是某一个实数,可以通过上面的等式实际算出来,不过这里主要是为了讲解解题的思路,所以没有将实际算出的数字标上
前面提到,此时乙与甲是在同一条边上的,那么它们之间的距离k肯定不能超出这条边的长度,即
$$0 < k = ax+b\leq80$$
根据上面的不等式就可以算出x的取值范围:
$$w_1 < x \leq w_2$$
则去x在该取值范围的最小正整数,通过它就可以知道此时甲到底位于哪个顶点,比如若此时x去3,则甲位于D点
Week-2
题目:
已知抛物线$y=x^2-2x-3$进过点A(-1,b),P(m,t)是抛物线上的一个动点,P关于原点的对称点为P’,问:
当点P’落在第二象限内,且$P’A^2$取得最小值时,求m的值
求解:
已知点P’是P关于原点的中心对称点,因此P’的坐标可以推出是(-m,-t),也可以求出点A的坐标为(-1,0)
又由于点P’落在第二象限,因此:
$$
\begin{cases}
-m<0 \\\ -t>0
\end{cases}
\to
\begin{cases}
m>0 \\
t<0
\end{cases}
$$
因为已知点A的坐标,也知道点P’坐标的表示方式,则可以将$P’A^2$表示出来:
$$
\begin{aligned}
P’A^2 &=(-m+1)^2+t^2 \\
&=m^2-2m+1+t^2
\end{aligned}
$$
虽然我们用m和t将$P’A^2$表示了出来,但是两个未知数还是太多,需要想办法消去其中一个,这时可以利用点P在抛物线上这个条件,则
$$
m^2-2m-3=t \to m^2-2m=t+3
$$
将这一步得到的结论$m^2-2m=t+3$带入上一步的结论中,从而得到
$$
P’A^2=t^2+t+1 (t<0)
$$
因此,此时题目的问题变成了:当t<0时,$P’A^2=t^2+t+1$在何处取到最小值?
很明显,抛物线$t^2+t+1$的开口向上,且其对称轴为$t=-\frac{1}{2}$,在抛物线的取值范围t<0上,因此t取$-\frac{1}{2}$
已经得到t的取值,将它带到抛物线表达式中,就可以将m求出了