1. 自然常数e
1.1. 什么是自然常数e?
以一个银行存款的例子简单描述一下:
复利:将本金存到银行,一段时间后结算存款利息,然后将利息和本金加在一起的本息,作为下一轮的本金来进行利息的结算
考虑一种理想状况,也就是假定有这样一家银行,它一年的存款利率是100% (简记为1),并允许我们自由选择结算利息的次数。如果我们存入银行1块钱,那么我们一年最多能够赚多少钱呢?
(1) 如果只在年底结算一次利息,由于一年的利率是1,那么一年后我们可以连本带利得到2块钱
$$1 \times (1 + 1) = 2 $$
(2) 如果我们要求每半年就结算一次利息,由于半年的利率是1/2,那么一年后我们可以连本带利得到2.25块钱
$$1 \times (1+\frac 12)^2=2.25$$
(3)如果我们要求每一个月就结算一次利息,由于一个月的利率是1/12,那么一年后我们可以连本带利得到2.61块钱
$$1 \times (1+\frac {1}{12})^{12}=2.61$$
可以看到,利息结算次数越多,年底获得的收入也就越多
如果我们脑洞大开,要求银行时时刻刻为我们结算利息,也就是说结算利息的次数为无数次,那么我们能否得到无穷无尽的收入,实现数钱数到手抽筋的梦想呢?
很遗憾,这个是不可能的!因为我们最终获得的收入其实就是下面这个式子
$$
\lim_{n\to+\infty}(1+\frac 1n)^n
$$
而数学家的计算已经表明,这个式子的值其实是有限的,其大小为2.718281828…,是一个无限不循环小数,为了使用方便,我们就用e来代表它
所以,e就是复利的极限,或者更广义地说,应该是增长的极限
1.2. e的指数函数$e^x$和对数函数lnx的重要性质——导数形式简单
这涉及到这两个函数的一些特殊性质
先讨论指数函数$y=a^x$
指数函数 $y=a^x$ 的导数为
$$
\frac{dy}{dx}=
\lim_{\Delta x \to 0}\frac{a^{x+\Delta x}-a^x}{\Delta x}=
a^x\lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x}
$$可以看到,要想得到$y=a^x$的导数,需要求得后面的极限,可是如果直接令$\Delta x \to 0$,是无法得到极限的
怎么办呢?
我们转换一下思维,让$a^{\Delta x}-1=\frac 1n$,则$\Delta x=\log_a(1+\frac 1n)$
于是上面的式子可以改写成
$$
\frac{dy}{dx}=
a^x\lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x}=
a^x\lim_{1/n \to 0}\frac{\frac 1n}{\log_a(1+\frac 1n)}=
a^x\lim_{n \to \infty}\frac{1}{\log_a(1+\frac 1n)^n}
$$这个时候我们发现,e的定义派上用场了:$\lim_{n\to+\infty}(1+\frac 1n)^n=e$
$$
\frac{dy}{dx}=
a^x\lim_{n \to \infty}\frac{1}{\log_a(1+\frac 1n)^n}=
a^x\frac{1}{\log_ae}
$$如果让$a=e$,则
$$\frac{d e^x}{dx}=e^x$$
接着讨论与指数函数$y=a^x$对应的另一半 $y=\log_ax$
我们来看一下$y=\log_ax$的导数
$$
\begin{aligned}
\frac{dy}{dx} &=
\lim_{\Delta x \to 0}\frac{\log_a(x+\Delta x)-\log_ax}{\Delta x} \\
&=\lim_{\Delta x \to 0}\log_a(\frac{x+\Delta x}{x})^{\frac{1}{\Delta x}} \\
&=\frac 1x\lim_{\Delta x \to 0}\log_a(\frac{x+\Delta x}{x})^{\frac{x}{\Delta x}} \\
&=\frac 1x\lim_{\Delta x \to 0}\log_a(1+\frac{\Delta x}{x})^{\frac{x}{\Delta x}} \\
&=\frac 1x\log_ae
\end{aligned}
$$如果我们让$a=e$,则
$$\frac{d\ln x}{dx}=\frac 1x$$
所以从上面可以看出,当a=e时,无论是指数函数还是对数函数,其导数形式都是最简单的
$$\frac{d e^x}{dx}=e^x ,\quad \frac{d\ln x}{dx}=\frac 1x$$
1.3. $e^x$ 和 lnx 的现实意义:拟合的需要
之所以频繁出现关于e的函数,是因为我们现实世界中有太多问题具有以下特点:即一个量的变化与自身大小相关,而凡是这一类问题,都迫使我们必须引入关于e的指数函数或对数函数,即拟合的需要
理想环境下的种群数量
在生物领域,一个简单而又经典的问题便是理想环境下的种群数量变化规律
种群数量越大,种群的增长速率也就越快,种群数量的变化率是和当前种群数量y相关的,于是可以简单描述为
$$\frac{dy}{dt}=\lambda y$$
我们已经知道,导数等于自身的函数就是$y=e^t$。但是因为右边存在一个比例常数$\lambda$,所以我们可以假定种群数量y随时间t的变化规律符合通用关系$y=ae^{bt}+c \quad (a≠0)$,从而有
$$abe^{bt}=\lambda ae^{bt}+\lambda c$$
要使等式两边相等,则需要$\lambda=b,\,c=0$
所以,理想环境下的种群数量变化符合规律:$y=ae^{\lambda t}$
我们知道,现实中的资源不可能无穷无尽,种群数量也不可能无限增长,可是上述规律却为我们研究早期某一种群数量的变化提供了一个良好的近似
弹簧振子的运动
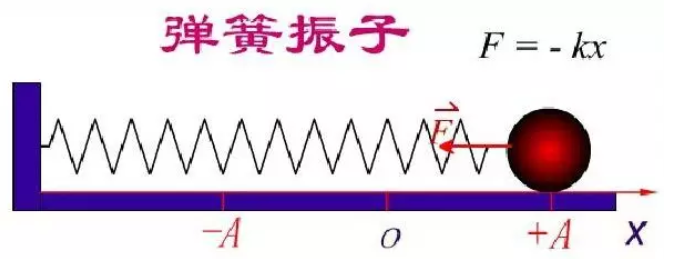
弹簧振子的受力和它自身的位移成正比,并且与运动方向相反
根据牛顿第二定律,有
$$m\frac{d^2x}{dt^2}=-kx$$
其中,$d^2x/dt^2$表示x对于t的二阶导数,相当于$d(dx/dt)/dt=dv/dt=a$,位移x对时间t的二阶导数就是加速度a
上式这么写还不是很明显,可以改写成下面这样
$$\frac{d^2x}{dt^2}=-\frac km x$$
由于弹簧和物体都是固定的,所以$k$和$m$都是常数,因此可以令$\lambda=-k/m$,所以上面的式子可以进一步改写成
$$\frac{d^2x}{dt^2}=\lambda x$$
也就是说,位移的二阶导与当前的位移成正比
而我们前面已经知道了,e的指数函数$e^x$不论进行几阶求导,它的导数都是它本身,所以,我们可以用通式 $x=ae^{bt}+c\quad (a\neq 0)$去拟合x与t的关系
那么
$$ab^2a^{bt}=\lambda ae^{bt}+\lambda c$$
要满足等式两边相等,需要让$\lambda=b^2,\,c=0$,即让$-k/m=b^2,\,c=0$,可以解出
$$b=\pm i\sqrt{\frac km}$$
所以弹簧振子的运动符合
$$x=a_1e^{\pm i\sqrt{k/m}}+a_2e^{\pm i\sqrt{k/m}}$$
2. 理解泰勒级数展开
泰勒级数的目的:
用一系列多项式相加的形式去组成多项式近似函数,来逼近光滑函数,比如$f(x)=\cos x$,从而在一定的精度要求下,通过对多项式函数的计算得到原始函数的近似计算结果,这种计算可以是原函数的计算,也可以是导数的计算,而且一般来说对多项式近似函数的计算的难度要远小于原函数
例如:
下面是$f(x)=\cos x$函数的图象
如何用多项式函数近似呢?
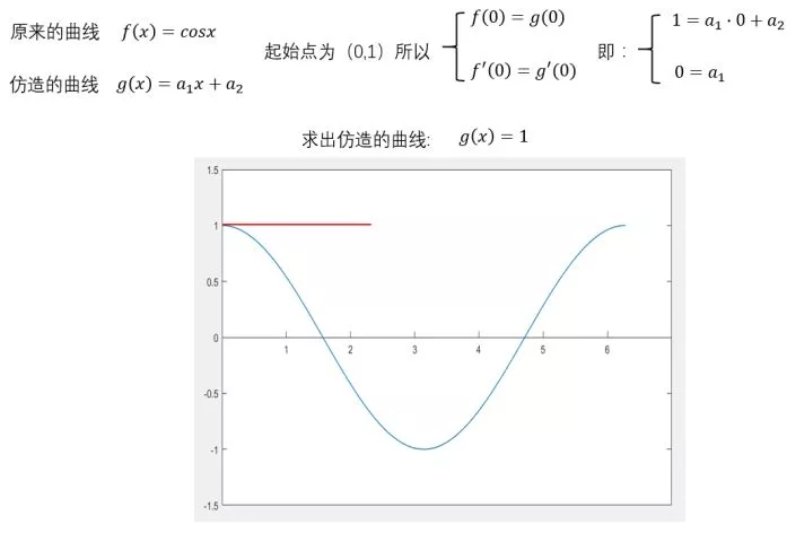
(1)首先得找一个切入点,可以是这条曲线最左端的点,也可以是最右端的点,anyway,可以是这条线上任何一点。比如选了最左边的点(0,1)
(2)让仿造的曲线也过这个点
(3)继续细节化,开始考虑曲线的变化趋势,即导数,保证在此处的导数相等
现在起始点相同了,整体变化趋势相近了,可能看起来有那么点意思了
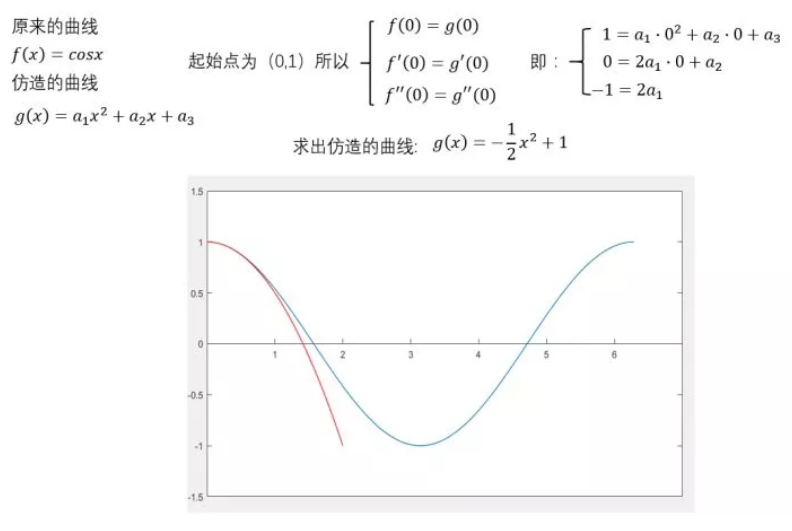
想进一步精确化,应该考虑凹凸性:高中学过:表征图像的凹凸性的参数为“导数的导数”。所以,下一步就让二者的导数的导数相等
起始点相同,增减性相同,凹凸性相同后,仿造的函数更像了。如果再继续细化下去,应该会无限接近。所以泰勒认为“仿造一段曲线,要先保证起点相同,再保证在此处导数相同,继续保证在此处的导数的导数相同……”
把刚才的思路翻译成数学语言,就变成了:
首先得让其初始值相等,即:$g(0)=f(0)$
其次,得让这俩函数在x=0处的导数相等,即:$g′(0)=f′(0)$
再次,得让这俩函数在x=0处的导数的导数相等,即:$g″(0)=f″(0)$
……
最终,得让这俩图像在x=0的导数的导数的导数的……的导数也相同
思考两个问题:
余弦函数能够无限次求导,为了让这两条曲线无限相似,我仿造出来的 g(x)必须也能够无限次求导,那g(x)得是什么样类型的函数呢?
实际操作过程中,肯定不能无限次求导,只需要求几次,就可以达到我想要的精度。那么,实际过程中应该求几次比较合适呢?
综合考虑这两个问题以后,泰勒给出了一个比较折中的方法:令 g(x)为多项式
多项式能求几次导数呢?视情况而定,比如五次多项式
$$f(x)=ax^5+bx^4+cx^3+dx^2+ex+f$$
能求5次导,继续求就都是0了,几次多项式就能求几次导数
泰勒比我们厉害的地方仅仅在于他想到了把这种生活经验、翻译成数学语言、并运用到仿造函数图像之中。假如告诉你这种思路,静下心来你都能自己推出来
下面咱们来简单的算一下前面的几阶导数,看看有什么规律:
先算个一阶的:
可以看出,除了在 (0,1)这个点,其他的都不重合
再来个二阶的:
可以看出,在 (0,1)这个点附近的一个小范围内,二者都比较相近
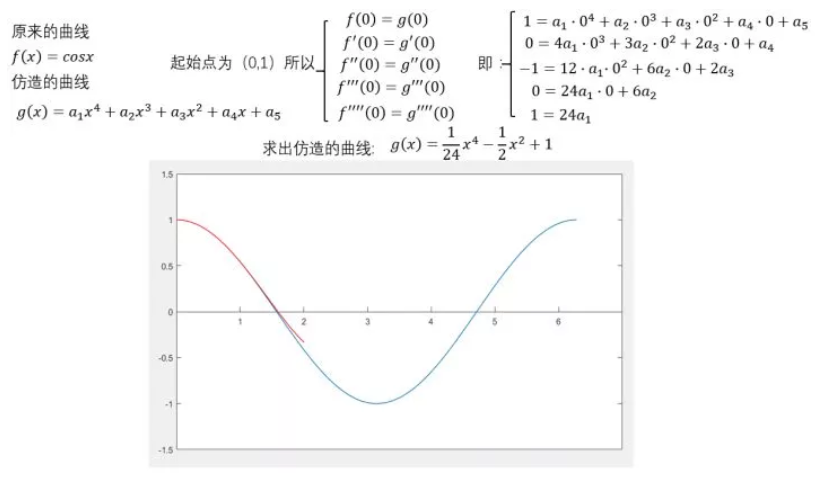
再来个四阶的
可以看出,仍然是在 (0,1)这个点附近的一个范围内二者很相近。只是,此时二者重合的部分扩大了
推到这里,我们大概想象得到,如果继续继续提高阶数,相似范围继续扩大,无穷高阶后,整个曲线都无限相似
将这种计算过程推广到n阶:
首先要在曲线 f(x) 上任选一个点,为了方便,就选 (0,f(0)),设仿造的曲线的解析式为g(x) ,前面说了,仿造的曲线是一个多项式,假设算到n阶
能求n次导数的多项式,其最高次数肯定也为n。所以,仿造的曲线的解析式肯定是这种形式:
$$g(x)=a_0+a_1x+a_2x^2+…+a_nx^n$$
前面说过,必须保证初始点相同,即$g(0)=f(0)=a_0$,求出了$a_0$
接下来,必须保证n阶导数依然相等,即$g^{(n)}(x)=f^{(n)}(x)$
因为对 g(x)求n阶导数时,只有最后一项为非零值,为$n!a_n$
由此求出:
$$a_n=\frac{f^{(n)}(x)}{n!}$$
综上:
$$g(x)=f(0)+\frac{f^{(1)}(0)}{1!}x+\frac{f^{(2)}(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n$$
不一定非要从x=0的地方开始,也可以从$(x_0,f(x_0))$开始,此时,只需要将0换成,然后再按照上面一模一样的过程重新来一遍,最后就能得到如下结果:
$$g(x)=f(x_0)+\frac{f^{(1)}(x_0)}{1!}(x-x_0)+\frac{f^{(2)}(x_0)}{2!}(x-x_0)^2+…+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$$
参考资料: