1. 背景知识
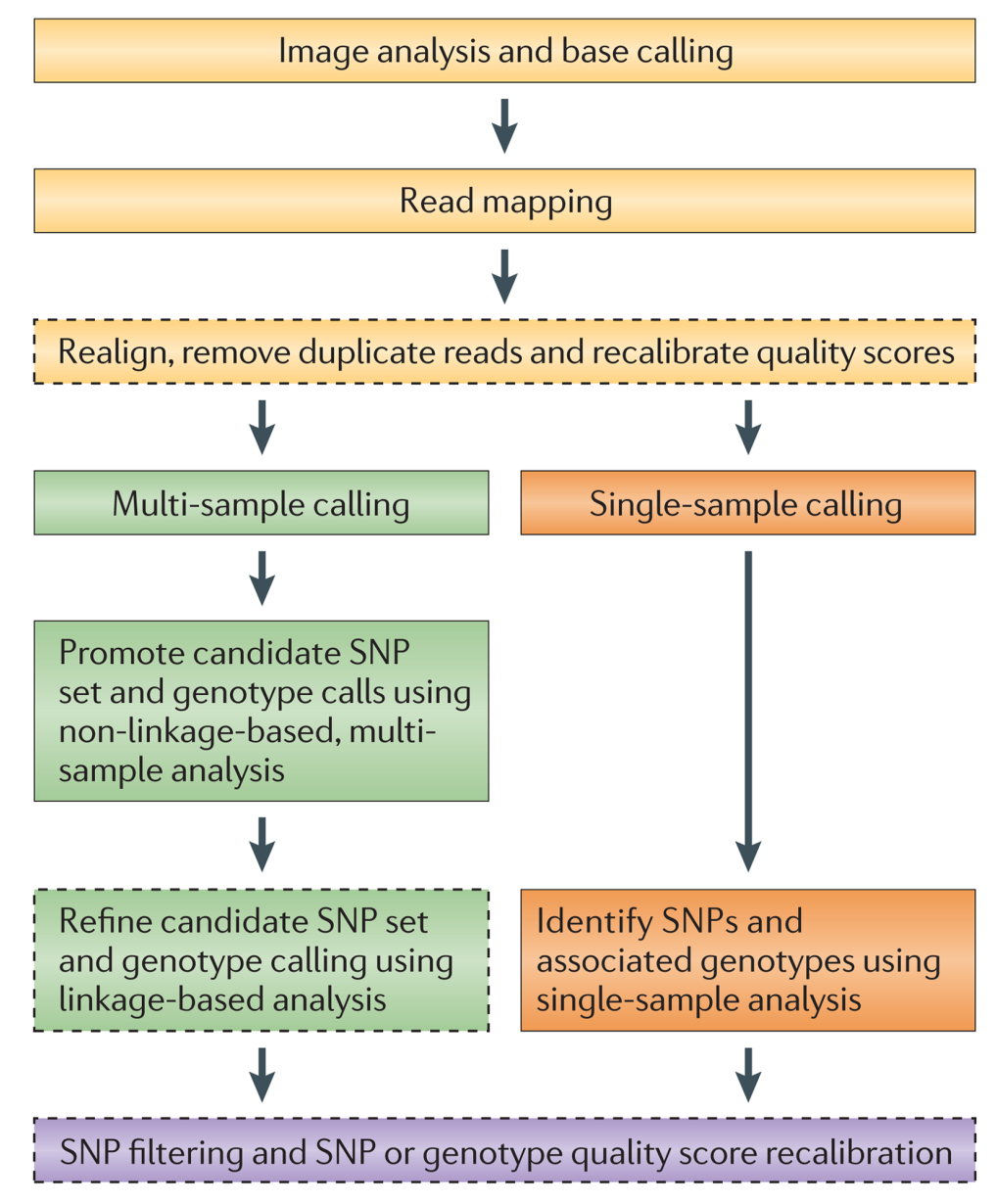
变异检测的常规步骤:
- 将一个或多个样本的reads比对到参考基因组;
- SNP calling:检出变异位点;
- genotype calling:鉴定出个体的每个变异位点的基因型 (genotype);
影响变异检测准确性的因素:
- base-calling 的错误率;
- 比对 (alignment) 的错误率;
- 低覆盖度的测序 (low-coverage sequencing, <5× per site per individual, on average),这使得:对于二倍体个体的两条同源染色体的某个位点,有很大概率只采样到其中一条染色体;
变异检测的准确率会影响到下游的分析,包括:
- 鉴定罕见变异 (rare mutations)
- 评估 allele 频率
- 相关性分析 (association mapping)
一个提高准确率的策略是进行靶向深度测序(sequence target regions deeply (at >20× coverage))
但是,随着大样本检测需求的增加,中覆盖度 (5-20X) 或 低覆盖度 (<5X) 是一个更加经济的选择。而且对于人群中低频变异的检测,大样本是一个重要前提,低覆盖度对低频变异检测的影响不大;对于相关性分析 (GWAS),依赖于大样本和每个样本鉴定的准确性,但是往往这两者是不可兼得的,那么相对于单样本鉴定的准确性来说,大样本更加重要
许多用于提高变异检测准确性和评估准确率的方法被陆续提出,这些方法大都采用了概率统计模型
对一个基本概率统计量 “genotype likelihoods” 进行建模
genotype likelihoods:包含了对 base calling,alignment 和 assembly 步骤中的错误率的综合评估,它利用了 allele frequencies、LD(连锁不平衡)模式等先验信息 (prior information)
最后给出的分析结果包括:
- SNP call 和对应的不确定性评估
- genotype call 和对应的不确定性评估
它们都有具体的统计学意义
1.1. base calling过程的错误及校正
不同测序仪的错误类型及产生的原因
(1)454测序仪——indel错误
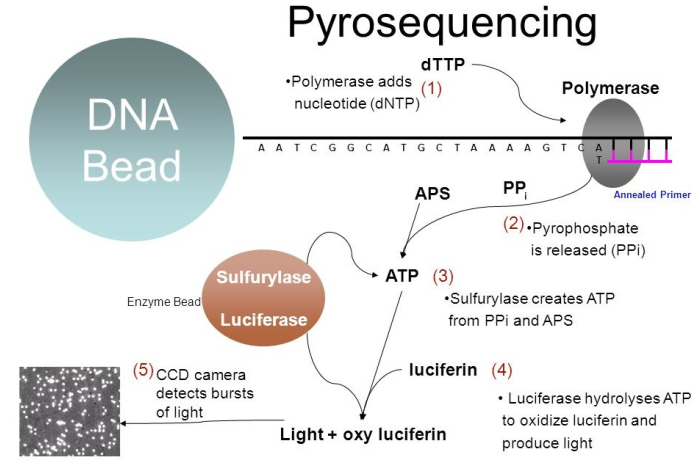
454采用的是焦磷酸测序法,每一轮测序加入一种 ddNTP 作为反应的底物,即每一轮反应连接上的碱基组成是已知的,如果这种 ddNTP 可以在当前位点与模板链互补则成功连接延伸,释放出焦磷酸而发出荧光,从而测出当前位点的碱基组成,否则不发荧光
但是如果在当前位点和它之后的若干个位点的碱基组成相同,即是同聚物形式,则当前这轮的测序反应是这几个连续位点的连续反应,由于这个连续反应之间的时间间隔几乎可以忽略不仅,则相当于一次性释放出多个焦磷酸,产生比单个反应强得多的荧光
由于前面已经提到,这轮反应检测的碱基组成是已知的,所以454测序的 base calling 过程要做的是区别这种同聚反应的同聚物的长度,理论上长度越长,荧光强度越高,但是实际上,同聚物长度与荧光强度之间并不存在稳定的正比关系,相同长度的同聚物产生的荧光强度具有较大的方差,这使得 base calling 过程容易产生较高比例的 indel 错误
(2)Illumina测序仪
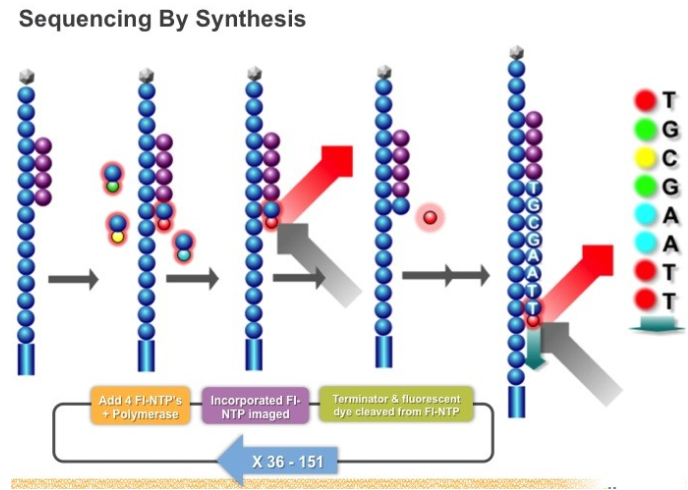
Illumina测序仪由于测序原理与454不同,它采用的是边合成边测序的原理,每成功加上一个碱基之后,由于刚加上的 ddNTP 的3号位被连接上了荧光基团,阻止了下一个 ddNTP 的连接,只有在被检测完荧光并且将占位的荧光基团切除后才能进行后面的合成反应,所以每次只能最多只有一个碱基的合成,因此不存在454中所谓的 indel 错误
Illumina 测序仪的 base calling 的错误主要来自于根据检测到的荧光推断出当前连接的碱基的组成这一步,称为 miscall,在当时(2010年附近),Illumina 测序仪的 miscall error rate 在 1% 附近
导致 miscall 的主要原因是同一个cluster(在测序芯片即flowcell上,一个cluster一般来说是来源于同一个ssDNA片段的扩增产物)中的不同的DNA片段合成过程的不同步
在每一轮反应中,大多数DNA片段是同步的,只有少数片段本来应该进行连接延伸,但是由于一些原因,比如部分反应空间ddNTP的浓度偏低,导致反应成功率下降,使得它的反应没有成功进行而相对于这个cluster的其他片段滞后了一些,或者,在曝光检测之后的荧光切除过程中有少部分的DNA片段上的荧光基团没有被成功切除,导致了后续反应的滞后,一般来说,第二种情况发生的可能性会大一些
因为每一轮不同步滞后的那些DNA片段毕竟占少数,所以,对这个cluster整体的荧光信息的影响比较小,所以在测序反应刚开始的时候,base calling 的准确率是比较高的;但是随着反应的持续进行,不同步部分不断累积越来越多,那么干扰信息也就越来越强,也就越来越难判断当前碱基组成到底是哪个,这也就解释了为什么反应越到后面测序质量越差
Phred 质量值校正
碱基质量的表示方式:Phred quality score (Q score)
$$Q_{Phred}=-10\log_{10} P(error)$$
则可以根据Q值算出它的实际错误率:
$$P(error)=10^{-Q/10}$$
若 Phred score 等于20,意味着测序错误率为 1%
Phred碱基质量值是由base-calling算法评估出来的,但是它们可能并不能准确地反映真实的base-calling错误率
针对不同测序平台提出 的 base calling 算法,包括:
454 —— Pyrobayes
SOLiD —— Rsolid
Illumina —— Ibis、BayesCall
这些 base calling 算法基本都是测序仪厂家开发出来的,将原始测序错误率降低了 ~5-30%
(1)SOAPsnp的校正策略
1.2. 比对过程的错误及校正
(1)比对过程中可能存在的问题
比对过程需要区分测序错误和实际的碱基差异,同时给出合适的比对质量值 (well-calibrated mapping quality values),因为后续的 variant calling 需要利用到它来计算后验概率 (posterior probabilities)
在进行比对的过程中,选择合适的mismatch位点数是一个比较重要的问题,它需要在准确性和read depth之间做权衡 (trade-off)
不同物种它适用的可容忍的mismatch数是不一样的
例如,果蝇不同个体之间的基因组变异程度相对于我们人来说是比较大的,如果用适用于人基因组mapping的可容忍mismatch数来进行果蝇基因组的mapping,明显是过于严格的,这样会导致大量的reads无法成功比对到参考基因组上,特别是那些多态性位点分布密度比较高的区域,reads基本上很难比对上,这些区域的变异的检出率也就比较低
再比如,将果蝇的参数用在人上面,那么比对的标准相对设低了,这就容易带来大量的错误比对结果
对于基因组中的高变区域,reads的mapping很困难,一个解决方案是使用更长的reads或者双端测序,但是对于diversity极高的区域,比如 MHC (major histocompatibility complex ) 区域,这些方法还是显得力不从心,这个时候就采用 de novo 拼接的策略了
结合长reads和de novo 拼接的方法,基因组中高变区域鉴定的大多数情况都可以得到有效地解决
2. SNP calling中的数学原理
2.1. 基于贝叶斯方法
符号说明:
| Symbol | Description |
|---|---|
| $n$ | Number of samples |
| $m_i$ | Ploidy of the $i$-th sample ($1≤i≤n$),即i样本的倍型 |
| $M$ | Total number of chromosomes in samples: $M=\sum_i m_i$ |
| $d_i$ | Sequencing data (bases and qualities) for the $i$-th sample |
| $g_i$ | Genotype (the number of reference alleles) of the $i$-th sample ( $0≤g_i≤m_i$ ) |
| $\phi_k$ | Probability of observing k reference alleles ( $\sum_{k=o}^M \phi_k=1$ ) |
| $Pr{A}$ | Probability of an event A |
| $L_i(\theta)$ | Likelihood function for the $i$-th sample: $L_i(\theta)=Pr{d_i \mid \theta}$ |
前提假设:
- 不同位点间相互独立;
- 对于同一个位点,不同reads的测序错误或mapping误差相互独立;
- 只考虑二等位情况;
估计某个样本出现特定基因型g的概率:$L(g)$
对于某一个样本的某一个位点,有$k$条 reads 比对上,其中有$l$条 ($0 \le l\le k$) 序列在该位点的碱基组成与 reference 一致,剩余 $k-l$ 条与 reference 不同,其中第 $j$ 条上该碱基的测序错误率为 $\epsilon_j$,则该样本的基因型与ref一致的有 $g \in [0,m]$ 种的概率为
$$
\begin{aligned}
&\quad L(g) \\
&= Pr(d \mid g) \\
&= \prod_{i=1}^l Pr_i(A)\prod_{j=l+1}^k Pr_j(\overline A) & (1)\\
&= \prod_{i=1}^l [Pr_i(B , A)+Pr_i(\overline B , A)]\prod_{j=l+1}^k [Pr_j(B , \overline A)+Pr_j(\overline B , \overline A)] & (2)\\
&= \prod_{i=1}^l [Pr_i(B,C) + Pr_i(\overline B,\overline C)] \prod_{j=l+1}^k [Pr_j(B,\overline C) + Pr_j(\overline B,C)] & (3)
\end{aligned}
$$其中,$m$ 是该物种的倍性,普通人是二倍体,因此一般 $m=2$
事件$A={测序碱基与\text{ref}一致}$,则$\overline A={测序碱基与\text{ref}不一致}$
事件$B={该碱基的测序是正确的}$,则$\overline B={该碱基的测序是错误的}$
事件$C={实际碱基与\text{ref}一致}$,则$\overline C={实际碱基与\text{ref}不一致}$
上面公式中,从(2)到(3)的推导涉及到最基本的逻辑常识,这里就不再赘述了
由于测序错误与基因组的组成无关,即$B \bot C$,因此上面的公式可以向下继续推导:
$$
\begin{aligned}
&= \prod_{i=1}^l [Pr_i(C)Pr_i(B) + Pr_i(\overline C)Pr_i(\overline B)] \prod_{j=l+1}^k [Pr_j(\overline C)Pr_j(B) + Pr_j(C)Pr_j(\overline B)] & (4)\\
&= \prod_{i=1}^l \left[ \frac{g}{m}(1-\epsilon_i) + \frac{m-g}{m}\epsilon_i \right] \prod_{j=l+1}^k \left[ \frac{m-g}{m}(1-\epsilon_j) + \frac{g}{m}\epsilon_j\right] & (5)\\
&= \frac{1}{m^k}\prod_{i=1}^l [g(1-\epsilon_i) + (m-g)\epsilon_i] \prod_{j=l+1}^k [(m-g)(1-\epsilon_j) + g\epsilon_j] & (6)
\end{aligned}
$$上面公式中,(4)到(5)的推导利用了:
$$
\begin{aligned}
&Pr(B)=1-\epsilon, \quad Pr(\overline B)=\epsilon & (7)\\
&Pr(C)=\frac gm , \quad Pr(\overline C)=\frac{m-g}{m} & (8)
\end{aligned}
$$(7)公式很好理解,在这里就不作更多的解释
对公式(8),下面作一下简单的解释:
由于上面的前提假设中就已经提到,只考虑双等位情况,ref allele即是双等位中的一种,则对于一个m倍体的个体,它该等位基因座上有m个等位基因,其中与ref allele一致的有g个,则剩下m-g个基因座上的allele与ref allele不一致
则,随机从这m个基因座中抽一个,其基因型与ref一致的概率为$Pr(C)=g/m$,与ref不一致的概率为$Pr(\overline C)=1-g/m=(m-g)/m$
估计某一个位点的allele frequency:$\psi$
假设某一个位点与ref一致的allele的频率为$\psi$,从多个样本的测序数据中估计出这个频率的数值,基本思想为:
推导出$Pr(D\mid \psi)$的表达式
然后基于极大似然估计(如下)来求出$\psi^{*}$
$$\psi^{*} = \arg \max_{\psi} Pr(D\mid \psi)$$
对于第i个样本,它的倍型为$m_i$,基因型为$g_i$,测序数据为$d_i$,根据HWE(Hardy-Weinberg,哈迪-温伯格法则,简称哈温平衡):
哈迪-温伯格(Hardy-Weinberg)法则
核心思想:一个不发生突变、迁移和选择的无限大的相互交配的群体中,基因频率和基因型频率将逐代保持不变
哈迪-温伯格定律可分为3个部分:
(1)在一个无穷大的随机交配的群体中,没有进化的压力(突变、迁移和自然选择);
(2)基因频率逐代不变;(3)随机交配一代以后基因型频率将保持平衡:
$p^2$表示AA的基因型的频率,$2pq$表示Aa基因型的频率$q^2$表示aa基因型的频率。其中p是A基因的频率;q是a基因的频率。基因型频率之和应等于1,即$p^2+ 2pq + q^2 = 1$
在该位点与ref一致的allele的频率为$\psi$情况下,出现我们的测序数据D的概率,即$\psi$的似然为:
$$
\begin{aligned}
&\quad L(\psi)\\
&= Pr(D \mid \psi ) \\
&=\prod_{i=1}^n Pr_i(d_i \mid \psi) & (1)\\
&=\prod_{i=1}^n \sum_{g=0}^{m_i} Pr_i(d_i,g \mid \psi) & (2)\\
&= \prod_{i=1}^n \sum_{g=0}^{m_i} Pr_i(d_i \mid g)Pr_i(g\mid \psi) & (3)\\
&= \prod_{i=1}^n \sum_{g=0}^{m_i} L_i(g)Binomial(g,m_i,\psi) & (4)\\
&= \prod_{i=1}^n \sum_{g=0}^{m_i} L_i(g) \left(\begin{matrix} m_i \\ g\end{matrix}\right) \psi^g(1-\psi)^{m_i-g} & (5)
\end{aligned}
$$上面公式中第(3)步到第(4)步的推导,利用了$Pr(g \mid \psi)=Binomial(g,m,\psi)$,即对于某一个$m$倍体样本,在群体的ref allele频率为$\psi$的情况下,它与ref allele一致的allele数为g的概率,这相当于在进行m重伯努利实验:
由于只考虑双等位型,则可以把ref allele 记为A,不一致的allel记为a,且$Pr(A)=\psi,Pr(a)=1-\psi$,则对于一个m倍体的个体,其ref allele的数量为g,则它的基因型为$A_1A_2…A_ga_{g+1}a_{g+2}…a_{m}$
在哈温平衡的理想群体中,这样基因型的个体可以看作是由m次伯努实验得到g次结果为1的事件得到的,则出现这样的事件的概率就为
$$Binomial(g,m,\psi)=\left(\begin{matrix} m \\ g\end{matrix}\right) \psi^g(1-\psi)^{m-g}$$
下面可以通过极大似然估计来得到ref allele的频率$\psi$:
$$\psi^* = \arg \max_{\psi} L(\psi)$$
由于
$$L(\psi)=\prod_{i=1}^n \sum_{g=0}^{m_i} L_i(g) \left(\begin{matrix} m_i \\ g\end{matrix}\right) \psi^g(1-\psi)^{m_i-g}$$
其中含有隐变量g,所以我们要进行的是含有隐变量的极大似然估计
对于含有隐变量的极大似然估计,首选的最优化方法一般是EM算法,其中第t步到第t+1步的迭代关系式为:
$$\psi^{(t+1)}=\frac 1M \sum_{i=1}^n \frac{\sum_g gL_i(g)Binomial(g,m_i,\psi^{(t)})}{\sum_g L_i(g)Binomial(g,m_i,\psi^{(t)})}$$
估计non-reference alleles的数量
首先定义一个名词:
site reference allele count:在一个位点上与ref allele一致的allele的数量,则对于样本i来说,它的site reference allele count可以记作$G_i$
定义向量$\vec G=(G_1,G_2,…,G_n)$,表示所有样本在某一个位点的site reference allele count
$X=\sum_i G_i$表示所有样本的site reference allele count的总和
$$Pr(\vec G = \vec g \mid X=k)= \mathbb{I}(k=\sum_{i=1}^n g_i) \frac{\prod_{i=1}^n \left( \begin{matrix} m_i \\ g_i\end{matrix} \right)}{\left( \begin{matrix} M \\ k\end{matrix} \right)}$$
其中,$\mathbb{I}(k=\sum_{i=1}^n g_i)$中的$\mathbb{I}(·)$表示布尔函数,即$\mathbb{I}(True)=1 \, \text{or} \, \mathbb{I}(False)=0$,也可以用克罗内克函数(Kronecker delta function) $\delta_{··}$ 表示,不过为了避免引入不必要的复杂概念对后续推导过程的干扰,这里还是使用常规的布尔函数表示
则群体中site reference allele count 为k似然为:
$$
\begin{aligned}
&\quad L(k) \\
&=Pr(D \mid X=k) & (1)\\
&= \sum_{\vec g} Pr(D,\vec G = \vec g \mid X=k) & (2)\\
&= \sum_{\vec g} Pr(G = \vec g \mid X=k) Pr(D \mid \vec G = \vec g) & (3)\\
&= \sum_{\vec g} \left( \mathbb{I}(k=\sum_{i=1}^n g_i) \frac{\prod_{i=1}^n \left( \begin{matrix} m_i \\ g_i\end{matrix} \right)}{\left( \begin{matrix} M \\ k\end{matrix} \right)} \right)\left(\prod_{i=1}^n L_i(g_i)\right) & (4)\\
&= \frac{1}{\left( \begin{matrix} M \\ k\end{matrix} \right)} \sum_{\vec g} \left(\mathbb{I}(k=\sum_{i=1}^n g_i)\prod_{i=1}^n \left( \begin{matrix} m_i \\ g_i\end{matrix} \right) L_i(g_i)\right) & (5)
\end{aligned}
$$
参考资料:
(1) Nielsen R, Paul JS, Albrechtsen A, Song YS. Genotype and SNP calling from next-generation sequencing data. Nat Rev Genet. 2011;12(6):443–451.
(2) Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics. 2011;27(21):2987–2993.