1. Beta分布
1.1. Beta分布及其函数公式推导
如果随机变量 $X$ 服从参数为 $n$ 和 $p$ 的二项分布,那么它的概率由概率质量函数(对于连续随机变量,则为概率密度函数)为:
$$p(x)=\begin{pmatrix} n \\ x \end{pmatrix}q^x(1-q)^{n-x}\tag{1}$$
把 $(1)$ 表示为变量 $q$ 的函数,即只有 $q$ 这一个变量,写成如下形式
$$f(q)\varpropto q^a(1-q)^b\tag{2}$$
其中 $a$ 和 $b$ 是常量,$q\in(0,1)$
为了把 $(2)$ 变成一个分布,可以给它乘上一个因子,使它对 $q$ 从0到1积分为1即可,即
$$f(q) = kq^a(1-q)^b\tag{3}$$
令其积分为1
$$\int_0^1 f(q)\mathbf dq = \int_0^1 kq^a(1-q)^b \mathbf dq=k\int_0^1 q^a(1-q)^b \mathbf dq=1 \tag{4}$$
则
$$k=\frac{1}{\int_0^1 q^a(1-q)^b \mathbf dq}$$
记 $B(a+1,b+1)=\int_0^1 q^a(1-q)^b \mathbf dq$,则 $k=B(a+1,b+1)^{-1}$,所以
那么规范化后的 (2) 就是一个分布了
$$f(q;a+1,b+1) = \frac{1}{B(a+1,b+1)}q^a(1-q)^b\tag{5}$$
这就是Beta分布的最原始的来源
对(5)进行适当的改造:取$\alpha=a+1,\beta=b+1$,并将积分 $B(a+1,b+1)=\int_0^1 q^a(1-q)^b \mathbf dq$ 中的q改为t,我们就得到了我们在教材上看到的Beta函数了:
$$B(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1} \mathbf dt\tag{6}$$
另外,将(5)中的q改为x,则我们就得到了我们在教材上看到的Beta分布的函数:
$$f(x;\alpha,\beta) = \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\tag{7}$$
到这里我们已经完整地推出了Beta函数(公式(6))和Beta分布(公式(7))
1.2. Beta 函数和 Gamma 函数的关系
先做一下前期的推导:
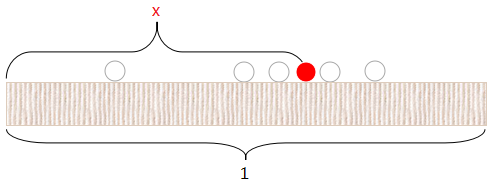
假设向长度为1的桌子上扔一个红球(如上图),它会落在0到1这个范围内,设这个长度值为 $x$ ,再向桌上扔一个白球,那么这个白球落在红球左边的概率即为 $x$。 若一共扔了 $n$ 次白球,其中每一次都是相互独立的,假设落在红球左边的白球数量为 $k$,那么随机变量 $K$ 服从参数为 $n$ 和 $x$ 的二项分布,即 $K∼b(n,x)$,有
$$P(K=k|x)=\begin{pmatrix} n \\ k \end{pmatrix}x^k(1-x)^{n-k}\tag{1}$$
$X$ 服从 $[0,1]$ 上的均匀分布,即 $X∼U[0,1]$
$K$ 对每一个 $x$ 都有上面的分布,对于所有可能的 $x$,$K$ 的分布为
$$P(K=k)=\int_0^1 \begin{pmatrix}n \\ k \end{pmatrix}x^k(1-x)^{n-k}\mathbf dx
=\begin{pmatrix}n \\ k \end{pmatrix}\int_0^1 x^k(1-x)^{n-k}\mathbf dx\tag{2}$$
现在,我们换一种方式来丢球:
先将这 $n+1$ 个球都丢出来,再选择一个球作为红球,任何一个球被选中的概率均为 $\displaystyle 1 \over n+1$,此时红球左边有 $0,1,2…n$ 个球的概率均为 $\displaystyle 1 \over n+1$,有
$$P(K=k)=\int_0^1 \begin{pmatrix}n \\ k \end{pmatrix}x^k(1-x)^{n-k}\mathbf dx
=\begin{pmatrix}n \\ k \end{pmatrix}\int_0^1 x^k(1-x)^{n-k}\mathbf dx=\frac{1}{n+1}$$则
$$\int_0^1 x^k(1-x)^{n-k}\mathbf dx=\frac{(n-k)!k!}{n!}\frac{1}{n+1}=\frac{k!(n-k)!}{(n+1)!}\tag{3}$$
再来看看$\Gamma$函数的定义:
$$\Gamma(m) = \int_0^{+\infty} e^{-x} x^{m-1} \mathbf dx=(m-1)!\tag{4}$$
那么,现在我们就可以推导出$\Gamma$函数与Beta函数的关系了:
由于
$$B(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1} \mathbf dt$$
根据(3),可令$k=\alpha-1,n-k=\beta-1\quad \Rightarrow \quad n=a+b-2$,则
$$B(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1} \mathbf dt=\frac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!}$$
又由于(4),可得
$$B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$$
因此,Beta分布也可以写成下面的形式:
$$f(x;\alpha,\beta) = \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}$$
1.3. Beta 分布的期望与方差
Beta 分布的期望
$$
\begin{aligned}
&\quad E[X] \\
&= \int_0^1 x f(x;\alpha,\beta) \\
&= \int_0^1 x \frac{x^{\alpha-1}(1-x)^{\beta-1}} {B(\alpha,\beta) } \mathbf dx \\
&= \frac{1} {B(\alpha,\beta) } \int_0^1 x^{\alpha}(1-x)^{\beta-1} \mathbf dx \\
&= \frac{B(\alpha+1,\beta)}{B(\alpha,\beta)} \\
&= \frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+\beta+1)}\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \\
&= \frac{\alpha}{\alpha+\beta}
\end{aligned}
$$Beta 分布的方差
由于Beta分布是概率密度分布,我们可以通过积分,得到它的概率分布函数
$$
\begin{aligned}
&\quad F(x) \\
&= \int_{-\infty}^x f(x)dx \\
&= \int_0^x \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1} dx \\
&= \frac{1}{B(\alpha,\beta)} \int_0^x x^{\alpha-1}(1-x)^{\beta-1} dx
\end{aligned}
$$定义$B(x,\alpha,\beta)=\int_0^x x^{\alpha-1}(1-x)^{\beta-1}$,称为不完全Beta函数(incomplete Beta function)则
$$F(x)=\frac{B(x,\alpha,\beta)}{B(\alpha,\beta)}$$
1.4. Beta分布与二项分布的关系
进行n次伯努利试验,其出现试验成功的概率p服从一个先验概率密度分布$Beta(\alpha,\beta)$,试验结果出现k次试验成功,则试验成功的概率p的后验概率密度分布为$Beta(\alpha+k,\beta+n-k)$
证明:
假设试验场景为棒球击球试验
该运动员击球时间的概率图模型如下图:
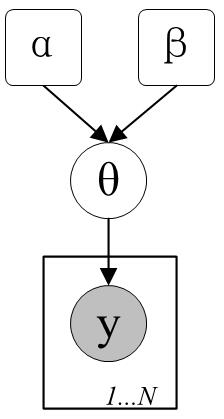
假设该用户的击球率的分布是一个参数为 $\theta$ 的分布(这里 $\theta$ 既表示一个分布,也是这个分布的参数。因为在概率图模型中,我们经常使用某个分布的参数来代替说明某个模型),也就是说 $\theta$ 是用户击球成功的概率
假设,到目前为止,用户在这个赛季总共打了 $n$ 次球,击中的次数是 $k$,结果记为 $y=(k,n)$ 这是一个二项式分布,即 $p(y \mid \theta) = \text{Binomial}(k;n,\theta)$($y$表示:总共打了 $n$ 次球,击中的次数是 $k$ 这个事件)
$y$是离散随机变量,则$y$服从的是概率质量函数(probability mass function)$P(y\mid n,\theta)=Binomial(k;n,\theta)$
$\theta$是连续随机变量,则$\theta$服从的是概率密度函数(probability density function)$p(\theta\mid \alpha,\beta)=Beta(\alpha,\beta)$
则$\theta$与$y$的联合概率密度函数为
$$
\begin{aligned}
&\quad f(\theta,y\mid \alpha,\beta) \\
&= f(\theta \mid \alpha,\beta)p(y \mid \theta) \\
&= \frac{1}{B(\alpha,\beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1} \begin{pmatrix}n \\ k\end{pmatrix}\theta^{k}(1-\theta)^{n-k} \\
&= \frac{1}{B(\alpha,\beta)}\begin{pmatrix}n \\ k\end{pmatrix}\theta^{\alpha+k-1}(1-\theta)^{\beta+n-k-1} \\
&= \frac{B(\alpha + k ,\beta + n -k)}{B(\alpha,\beta)}\begin{pmatrix}n \\ k\end{pmatrix} \frac{1}{B(\alpha + k ,\beta + n -k)}\theta^{\alpha+k-1}(1-\theta)^{\beta+n-k-1} \\
&= h(y)g(\theta,y)
\end{aligned}
$$
其中,
$$h(y)=\frac{B(\alpha + k ,\beta + n -k)}{B(\alpha,\beta)}\begin{pmatrix}n \\ k\end{pmatrix}$$
$h(y)$与$\theta$无关
$$g(\theta,y)=\frac{1}{B(\alpha + k ,\beta + n -k)}\theta^{\alpha+k-1}(1-\theta)^{\beta+n-k-1}$$
$g(\theta,y)$其实就是形状参数为$\alpha + k ,\beta + n -k$的Beta分布
现在,我们需要求出$\theta$在给定$y$情况下的后验分布$f(\theta\mid y,\alpha,\beta)$
由于$f(\theta,y\mid \alpha,\beta)=f(\theta\mid y,\alpha,\beta)f(y \mid \alpha,\beta)$,而其中的$f(\theta,y\mid \alpha,\beta)$就是上面我们推导出的$\theta,y$的联合概率密度分布,$f(y \mid \alpha,\beta)$是$y$的边际概率密度分布(marginal probability density function)
$$
\begin{aligned}
&\quad f(y \mid \alpha,\beta) \\
&= \int_{-\infty}^{\infty}f(\theta,y\mid \alpha,\beta)d\theta \\
&= \int_0^1 h(y)g(\theta,y)d\theta \\
&= h(y)\int_0^1 g(\theta,y)d\theta \\
&= h(y)
\end{aligned}
$$
因此
$$f(\theta\mid y,\alpha,\beta)=g(\theta,y)=Beta(\alpha + k ,\beta + n -k)$$
1.5. Beta分布与均匀分布的关系
当$\alpha=1,\beta=1$的时候,它就是一个均匀分布
$$
f(x;\alpha=1,\beta=1)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}=\frac{\Gamma(2)}{\Gamma(1)\Gamma(1)}x^0(1-x)^0=1
$$
参考资料:
(1) 潇水汀寒《认识Beta函数》