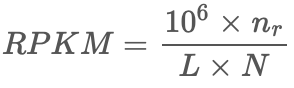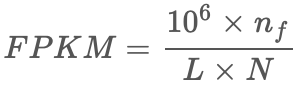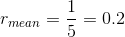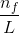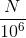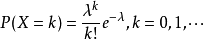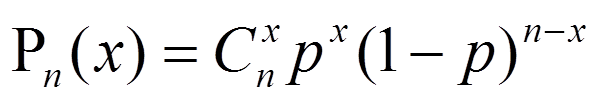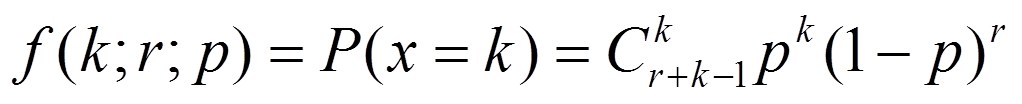数据预处理
过滤低表达的基因
所有数据集将包括表达的基因和不表达的基因的组合。 虽然检查在一种条件下表达但不在另一种条件下表达的基因是有意义的,但是一些基因在所有样品中都未表达
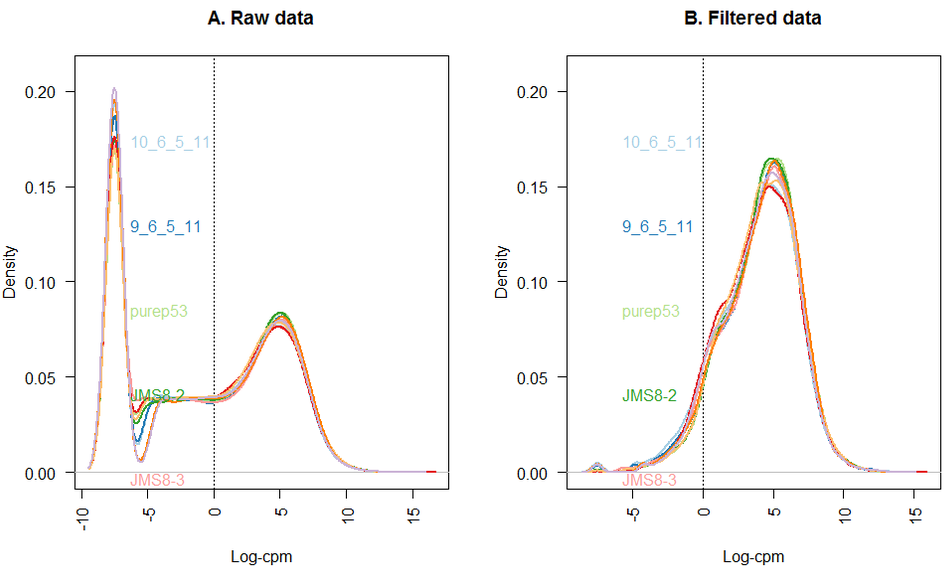
标准化
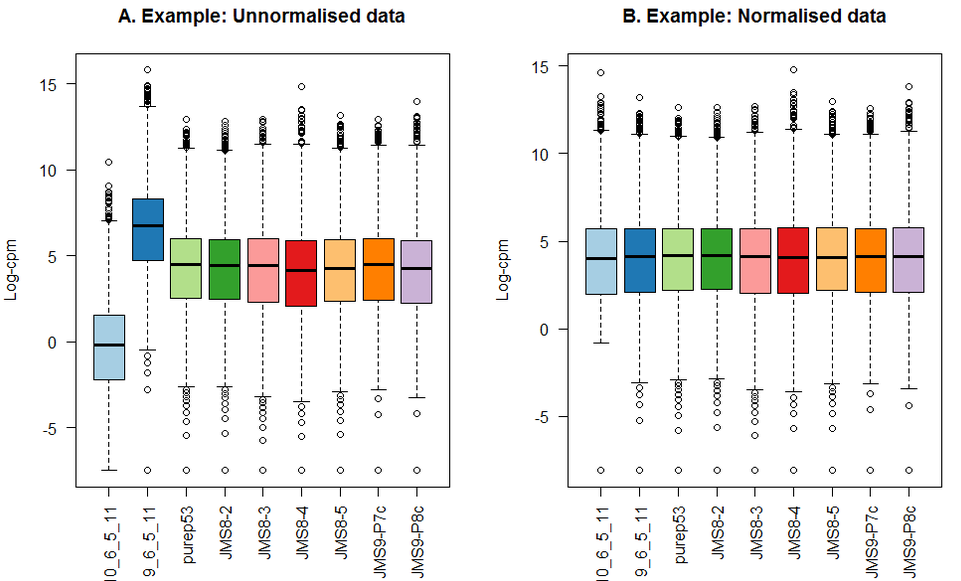
由于不同文库测序深度不同,比较前当然要进行均一化!用总reads进行均一化可能最简单,其基于以下两个基本假设:
- 绝大多数的gene表达量不变;
- 高表达量的gene表达量不发生改变;
但在转录组中,通常一小部分极高丰度基因往往会贡献很多reads,如果这些“位高权重”的基因还是差异表达的,则会影响所有其它基因分配到的reads数,而且,两个样本总mRNA量完全相同的前提假设也过于理想了。那如何比较呢,各个方家使出浑身解数,有用中位数的,有用75分位数的,有用几何平均数的,有用TMM(trimmed mean of Mvalues)的等等,总之要找一个更稳定的参考值。
House-keeping gene(s)
矫正的思路很简单,就是在变化的样本中寻找不变的量
那么在不同RNA-seq样本中,那些是不变的量呢?一个很容易想到的就是管家基因 (House-keeping gene(s))
那么 Human 常用的 House-keeping gene 怎么确定?
目前大家用的比较多的一个human housekeeping gene list 来源于下面这篇文章,是2013年发表在 Cell系列的 Trends in Genetics 部分的一篇文章

spike-in
使用Housekeeping gene的办法来进行相对定量,这种办法在一定程度上能够解决我们遇到的问题。但其实这种办法有一个非常强的先验假设:housekeeping gene的表达量不怎么发生变化。其实housekeeping gene list有几千个,这几千个基因有一定程度上的变化是有可能的
spike-in方法:在RNA-Seq建库的过程中掺入一些预先知道序列信息以及序列绝对数量的内参。这样在进行RNA-Seq测序的时候就可以通过不同样本之间内参(spike-in)的量来做一条标准曲线,就可以非常准确地对不同样本之间的表达量进行矫正
比较常用的spike-in类型:ERCC Control RNA
ERCC = External RNA Controls Consortium
ERCC就是一个专门为了定制一套spike-in RNA而成立的组织,这个组织早在2003年的时候就已经宣告成立。主要的工作就是设计了一套非常好用的spike-in RNA,方便microarray,以及RNA-Seq进行内参定量
CPM
CPM(count-per-million)
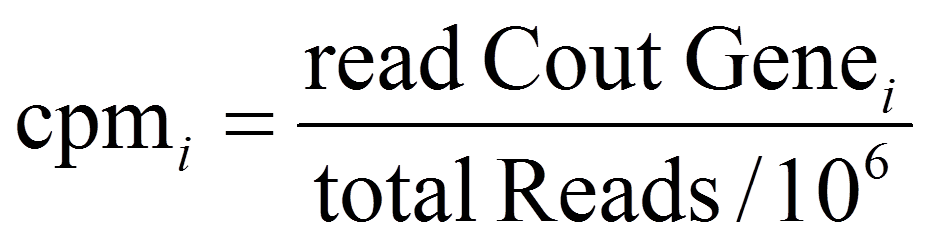
TCS (Total Count Scaling)
简单来说,就是找出多个样本中library size为中位数的样本,作为参考样本,将所有的样本的library size按比例缩放到参考样本的水平
选择一个library size为中位数的sample,以它为baseline,计算出其它sample对于baseline的normalization factor,即一个缩放因子:

然后基于该缩放因子对特定的sample中的每个基因的read count进行标准化(缩放):
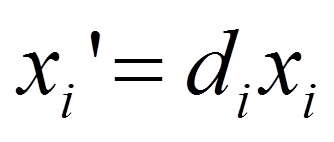
Quantile
简单来说,就是排序后求平均,然后再回序

在R里面,推荐用preprocessCore 包来做quantile normalization,不需要自己造轮子啦!
但是需要明白什么时候该用quantile normalization,什么时候不应该用,就复杂很多了
Median of Ratio (DESeq2)
该方法基于的假设是,即使处在不同条件下的不同个样本,大多数基因的表达是不存在差异的,实际存在差异的基因只占很小的部分那么我们只需要将这些稳定的部分找出来,作为标准化的内参,依据内参算出各个样本的标准化因子
(1)对每个基因计算几何平均数,得到一个假设的参考样本(pseudo-reference sample)
| gene | sampleA | sampleB | pseudo-reference sample |
|---|---|---|---|
| EF2A | 1489 | 906 | sqrt(1489 * 906) = 1161.5 |
| ABCD1 | 22 | 13 | sqrt(22 * 13) = 17.7 |
| … | … | … | … |
(2)对每个样本的每个基因对于参考样本计算Fold Change
| gene | sampleA | sampleB | pseudo-reference sample | ratio of sampleA/ref | ratio of sampleB/ref |
|---|---|---|---|---|---|
| EF2A | 1489 | 906 | 1161.5 | 1489/1161.5 = 1.28 | 906/1161.5 = 0.78 |
| ABCD1 | 22 | 13 | 16.9 | 22/16.9 = 1.30 | 13/16.9 = 0.77 |
| MEFV | 793 | 410 | 570.2 | 793/570.2 = 1.39 | 410/570.2 = 0.72 |
| BAG1 | 76 | 42 | 56.5 | 76/56.5 = 1.35 | 42/56.5 = 0.74 |
| MOV10 | 521 | 1196 | 883.7 | 521/883.7 = 0.590 | 1196/883.7 = 1.35 |
| … | … | … | … | … | … |
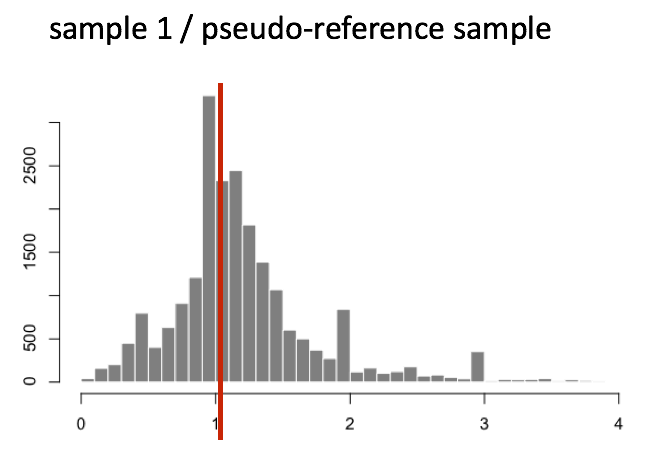
(3)获取每个样本中Fold Change的中位数,我们就得到了非DE基因代表的Fold Change,该基因就是我们选择的该样本的内参基因,它的Fold Change就是该样本的标准化因子
1 | normalization_factor_sampleA <- median(c(1.28, 1.3, 1.39, 1.35, 0.59)) |
TMM (Trimmed Mean of M value, edgeR)
该方法的思想与DESeq2的Median of Ratio相同,假设前提都是:大多数基因的表达是不存在差异的
它与DESeq2的不同之处在于对内参的选择上:
DESeq2选择一个内参基因,它的Ratio/Fold-Change就是标准化因子
edgeR选择一组内参基因集合,它们对标准化因子的计算均有贡献:加权平均
(1)移除所有未表达基因
(2)从众多样本中找出一个数据趋势较为平均的样本作为参考样本
对所有样本求总Read数;
各样本除以各自的总Read数,得到修正Read数;
求出各自样本修正Read数的Q3值(第3个四分位数);
所有的Q3值求平均,与平均Q3相差最小的样本即是参考样本。

(3)找出每个样本中的代表基因集,参考这些代表基因集的fold change,计算出该样本的标准化因子
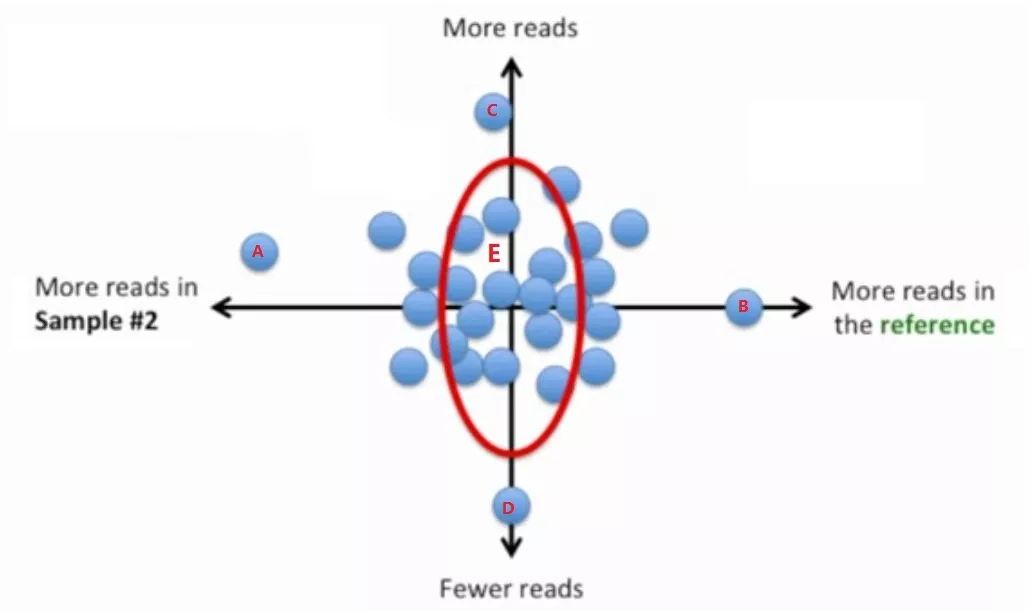
寻找样本的代表基因集:依据基因的偏倚程度和Reads数大小选出——偏倚程度小、reads数居中的基因
- 衡量偏倚度的量:LFC (log fold change)
LFC过大或过小都表示具有偏倚性,LFC越大表示reads数在samplei中越高,即偏向samplei;LFC越小表示reads数在ref中越高,即偏向ref
- 衡量reads数的量:read的几何平均数 (read geometric mean, RGM)
RGM越大表示基因reads越多,RGM越小表示基因reads越少
结合偏倚度、read数画出散点图:
偏倚度小、表达量居中的那些基因落在图中的红线附近
由参考代表基因集计算样本的标准化因子:
对这些代表基因集计算加权平均数:
该加权平均数就能代表该样本的标准化因子,只是经过了log变换,所以需要恢复为它的正值:
Scaling-Factor = 2 weight-average
为什么说FPKM和RPKM都错了?
FPKM和RPKM分别是什么
FPKM和RPKM分别是什么
RPKM是Reads Per Kilobase per Million的缩写,它的计算方程非常简单:
FPKM是Fregments Per Kilobase per Million的缩写,它的计算与RPKM极为类似,如下:
与RPKM唯一的区别为:F是fragments,R是reads,如果是PE(Pair-end)测序,每个fragments会有两个reads,FPKM只计算两个reads能比对到同一个转录本的fragments数量,而RPKM计算的是可以比对到转录本的reads数量而不管PE的两个reads是否能比对到同一个转录本上。如果是SE(single-end)测序,那么FPKM和RPKM计算的结果将是一致的。
这两个量的计算方式的目的是为了解决计算RNA-seq转录本丰度时的两个bias:
- 相同表达丰度的转录本,往往会由于其基因长度上的差异,导致测序获得的Read(Fregment)数不同。总的来说,越长的转录本,测得的Read(Fregment)数越多;
- 由测序文库的不同大小而引来的差异。即同一个转录本,其测序深度越深,通过测序获得的Read(Fregment)数就越多。
什么样才算好的统计量
首先,到底什么是RNA转录本的表达丰度这个问题
对于样本X,其有一个基因g被转录了mRNA_g次,同时样本X中所有基因的转录总次数假定是mRNA_total, 那么正确描述基因g转录丰度的值应该是:

则一个样本中基因表达丰度的均值为

而

所以

这个期望值竟然和测序状态无关!仅仅由样本中基因的总数所决定的
也就是说,对于同一个物种,不管它的样本是哪种组织(正常的或病变的),也不管有多少个不同的样本,只要它们都拥有相同数量的基因,那么它们的r_mean都将是一致的
由于上面的结果是在理论情况下推导出来的,实际上我们无法直接计算这个r,那么我们可以尝试通过其他方法来近似估计r,只要这些近似统计量可以隐式地包含这一恒等关系即可
FPKM和RPKM犯的错
实际数据来证明
假定有两个来自同一个个体不同组织的样本X和Y,这个个体只有5个基因,分别为A、B、C、D和E它们的长度分别如下:
r_mean值是:
如果FPKM或RPKM是一个合适的统计量的话,那么,样本X和Y的平均FPKM(或RPKM)应该相等。
以下这个表格列出的分别是样本X和Y在这5个基因分别比对上的fregment数和各自总的fregment数量:
可以算出:样本X在这5个基因上的FPKM均值FPKM_mean = 5,680;样本Y在这5个基因上的FPKM均值FPKM_mean = 161,840
很明显,它们根本不同,而且差距相当大
究竟为什么会有如此之大的差异?
可以从其公式上找到答案
首先,我们可以把FPKM的计算式拆分成如下两部分。
第一部分的统计量是对一个基因转录本数量的一个等价描述(虽然严格来讲也没那么等价):
第二部分的统计量是测序获得的总有效Fregment数量的百万分之一:
这么一拆,就可以看出这个公式的问题了:逻辑上根本说不通嘛!
尤其是第二部分(N/10^6),本来式子的第一部分是为了描述一个基因的转录本数量,那么正常来讲,第二部分就应该是样本的转录本总数量(或至少是其总数量的等价描述)才能形成合理的比例关系,而且可以看出来FPKM/RPMK是有此意的,这本来就是这个统计量的目的。
但是N/10^6并不能描述样本的转录本总数量。N/10^6的大小其实是由RNA-seq测序深度所决定的,并且是一个和总转录本数量无直接线性关系的统计量——N与总转录本数量之间的关系还受转录本的长度分布所决定,而这个分布往往在不同样本中是有差异的!
TPM是一个合适的选择
这个统计量在2012年所发表的一篇讨论RPKM的文章(RPKM measure is inconsistent among samples. Wagner GP, Kin K, Lynch VJ. Theory Biosci. 2012.)中就被提出来了,称之为TPM —— Transcripts Per Million,它的计算是:
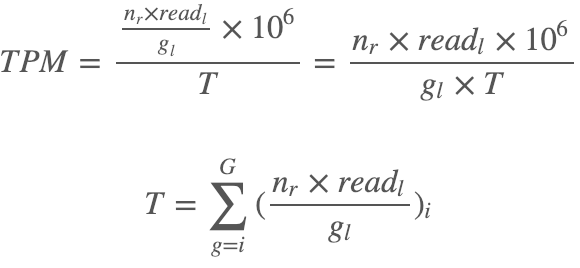
简单计算之后我们就可以发现TPM的均值是一个独立于样本之外的恒定值,它等于:
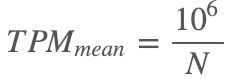
这个值刚好是r_mean的一百万倍,满足等价描述的关系。
统计学原理
转录组数据统计推断的难题
在RNA-seq中进行两组间的差异分析是最正常不过的了。
我们在其它实验中同样会遇到类似的分析,通常,我们可以用方差分析判定两组“分布”数据间是否存在显著差异。原理是:当组间方差大于组内方差(误差效应),并且统计学显著时,则认为组间处理是可以引起差异的。
有伙伴肯定要问,转录组数据到底有什么了不起的?它们为什么不能用我们熟悉的算法简单地进行计算?
其实统计学家也很无奈啊,看看我们转录组实验得到的这些数据吧:我们的实验只进行少得可怜的生物学重复(n<10),而且,任何基因的表达量都不能是负数,这些数据并不符合正态分布,用于表征表达量的counts是非连续的(芯片信号是连续的),RNA-seq数据的离散通常是高度扭曲的,方差往往会大于均值……,就这些奇怪的特征,使得准确估计方差并没有想象的那么容易。
我们面临两个核心问题:
- 基因表达数据适合用什么统计学分布进行差异显著性检验?
- 如何利用少量生物学重复数据估算基因表达的标准差?
泊松分布 or 负二项分布?
从统计学的角度出发,进行差异分析肯定会需要假设检验,通常对于分布已知的数据,运用参数检验结果的假阳性率会更低。转录组数据中,raw count值符合什么样的分布呢?
count值本质是reads的数目,是一个非零整数,而且是离散的,其分布肯定也是离散型分布。对于转录组数据,学术界常用的分布包括泊松分布 (poisson)和负二项分布 (negative binomial)两种。
为什么泊松分布不行?
首先有必要简单地介绍一下泊松分布
泊松分布适合于描述单位时间(或空间)内随机事件发生的次数(事件发生的次数只能是离散的整数)。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数,一块产品上的缺陷数,显微镜下单位分区内的细菌分布数等等。
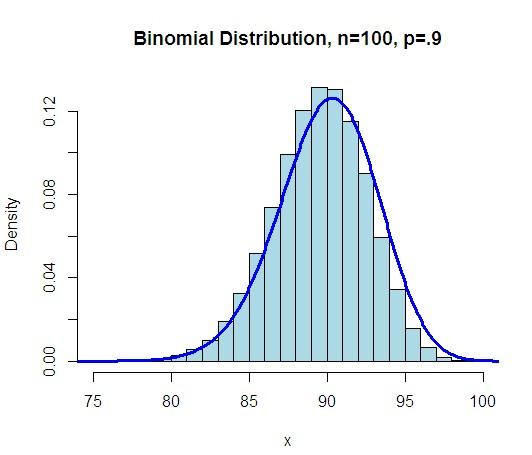
泊松分布大概长这样:
λ是波松分布所依赖的唯一参数。 λ值愈小分布愈偏倚, 随着λ的增大 , 分布趋于对称。 当λ=20时分布接近于正态分布;当λ=50时, 可以认为波松分布呈正态分布。
在数据分析的早期,确实有学者采用泊松分布进行差异分析,但是发展到现在,几乎全部都是基于负二项分布了,究竟是什么因素导致了这种现象呢?为了解释这个问题,我们必须提到一个概念 overdispersion。
dispersion指的是离散程度,研究一个数据分布的离散程度,我们常用方差这个指标。对于泊松分布而言,其均值和方差是相等的,但是我们的数据确不符合这样的规律。通过计算所有基因的均值和方差,可以绘制如下的图片:
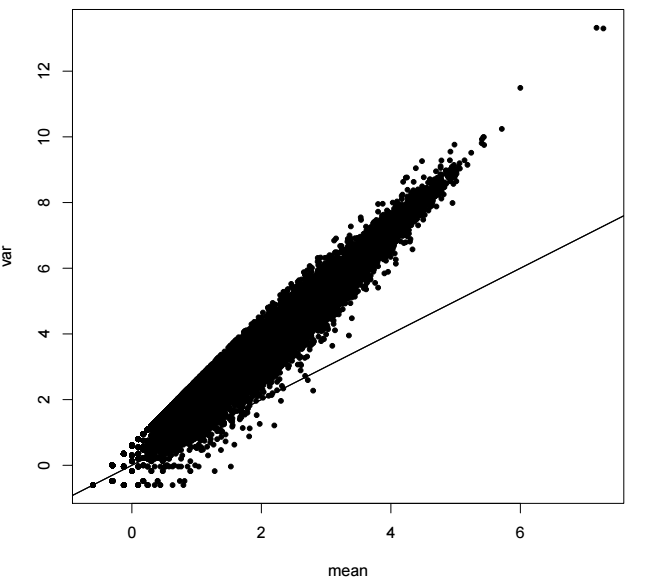
横坐标为基因在所有样本中的均值,纵坐标为基因在所有样本中的方差,直线的斜率为1,代表泊松分布的均值和方差的分布。可以看到,真实数据的分布是偏离了泊松分布的,方差明显比均值要大。
如果假定总体分布为泊松分布, 根据我们的定量数据是无法估计出一个合理的参数,能够符合上图中所示分布的,这样的现象就称之为overdispersion。
由于真实数据与泊松分布之间的overdispersion,选择泊松分布分布作为总体的分布是不合理。
以上只证明了泊松分布是个不太恰当的分布估计,那怎么证明负二项分布就是合适的分布估计呢?
为什么负二项分布行?
主要是从均值与方差之间的关系去证明
同样的,也先简单介绍一下负二项分布:
二项分布描述的是n重伯努利实验,在n重贝努利试验中,事件A恰好发生x(0≤x≤n)次的概率为:
它的概率分布图如下:
负二项分布描述的也是伯努利实验,不过它的目标事件变成了:对于Bernoulli过程,我们设定,当某个结果出现固定次数的时候,整个过程的数量,比如我们生产某个零件,假设每个零件的合格与否都是相互独立的,且分布相同,那么当我们生产出了五个不合格零件时,一共生产了多少合格的零件,这个数量就是一个负二项分布,公式如下:
该公式描述的是,在合格率为p的一堆产品中,进行连续有放回的抽样,当抽到r个次品时,停止抽样,此时抽到的正品正好为k个的概率
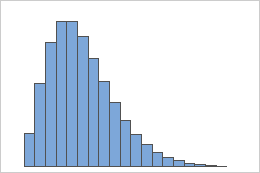
它的概率分布如下:
负二项分布的均值和方差分别为:
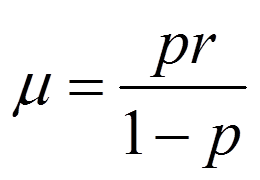
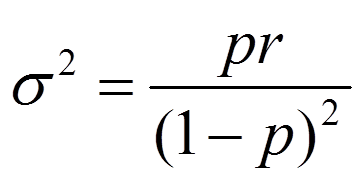
将p用μ表示,得到:

将上一步推出的p和1-p带入到方差的表达式中,得到:

记1/r=α,则
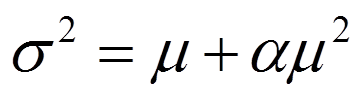
从上面的式子可以看出,均值是方差的二次函数,方差随着均值的增加而进行二次函数形式的递增,正好符合上文 2.2.1. 为什么泊松分布不行?部分均值与方差分布图的情况
其中α和r被称为dispersion parameter
负二项分布与泊松分布的关系,可以用α或r推出:
当
r -∞时,α -0,此时 σ2</sup= μ,为泊松分布;当
r -> 0时,α -> ∞,此时overdispersion
方差估计
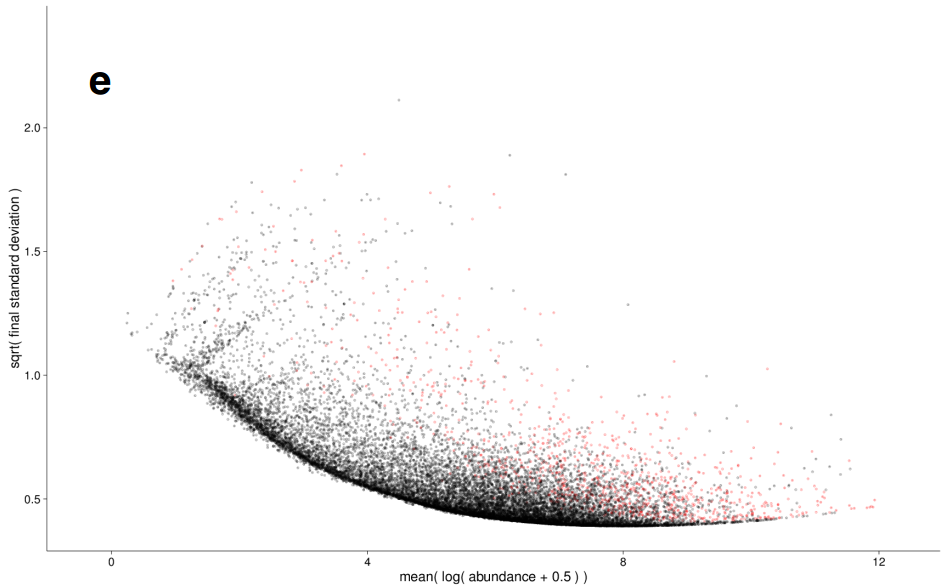
在生物学重复很少时,我们是很难准确计算每个基因表达的标准差的(相当于这个数据集的离散程度)。我们很可能会低估数据的离散程度。
被逼无奈的科学家提出了一个假设:表达丰度相似的基因,在总体上标准差应该也是相似的。我们把不同生物学重复中表达丰度相同的基因的总标准差取个平均值,低于这个值的都用这个值,高于这个值的就用算出来的值。
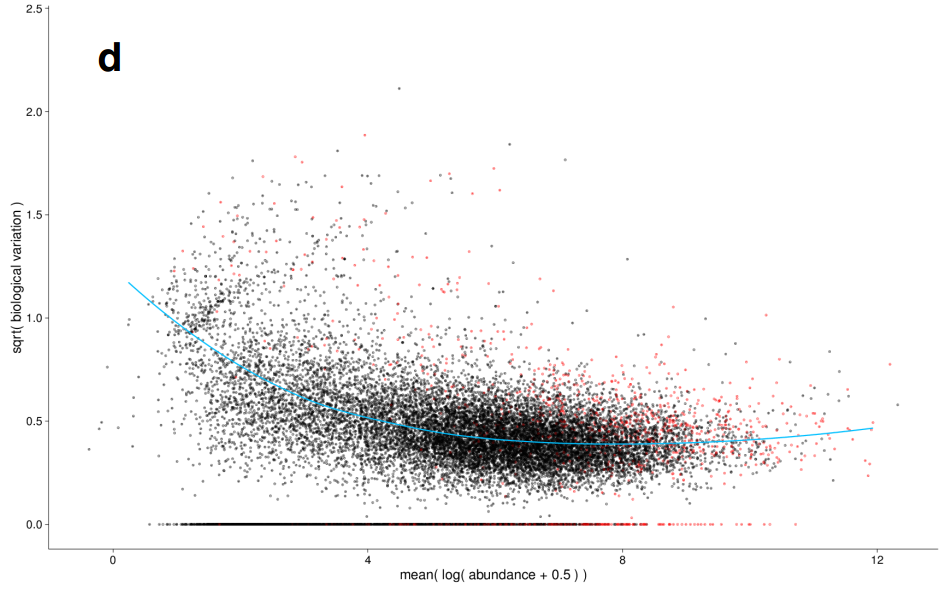
参考资料:
(1) 【生信菜鸟团】quantile normalization到底对数据做了什么?
(3) 生信菜鸟团:StatQuest生物统计学专题 - library normalization进阶之edgeR的标准化方法
(7) 【生信媛】RNA-seq分析中的dispersion,你知道吗?
(8) H. J. Pimentel, et al. Differential analysis of RNA-Seq incorporatingquantification uncertainty. bioRxiv, 2016