1. 奇异值分解 (SVD) 及其应用
1.1. SVD算法
矩阵A可以如下分解成三个矩阵的乘积:
$$
A_{MN}=X_{MM} \times B_{MN} \times Y_{NN}
$$
其中X是一个酉矩阵 (Unitary Matrix),Y则是一个酉矩阵的共轭矩阵
与其共轭矩阵转置相乘等于单位阵的矩阵是酉矩阵,因此酉矩阵及其共轭矩阵都是方阵
B是一个对角阵,即只有对角线上是非0值
维基百科上给出了下面的例子:
$$
A_{4 \times 5}=
\begin{bmatrix}
1 & 0 & 0 & 0 & 2 \\
0 & 0 & 3 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
0 & 4 & 0 & 0 & 0
\end{bmatrix}
\quad
X_{4 \times 5}=
\begin{bmatrix}
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & -1 \\
1 & 0 & 0 & 0
\end{bmatrix}
\quad
B_{4 \times 5}=
\begin{bmatrix}
4 & 0 & 0 & 0 & 0 \\
0 & 3 & 0 & 0 & 0 \\
0 & 0 & \sqrt{5} & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{bmatrix}
\quad
Y_{5 \times 5}=
\begin{bmatrix}
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
\sqrt{0.2} & 0 & 0 & 0 & \sqrt{0.8} \\
-\sqrt{0.8} & 0 & 0 & 0 & \sqrt{0.2}
\end{bmatrix}
$$
那么如何进行奇异值分解呢?
一般分两步进行:
(1)将矩阵A变换成一个双对角矩阵(除了两行对角线元素非零,剩下的都是零),这个过程的计算量为$O(MN^2)$,如果矩阵是稀疏的,那么可以大大缩短计算时间;
(2)将双对角矩阵变成奇异值分解的三个矩阵。这一步的计算量只是第一步的零头;
奇异值分解的一个重要目的是进行数据的低维度表示,即将$A_{MN}=X_{MM} \times B_{MN} \times Y_{NN}$ 转换为 $A_{MN}=X_{Mn} \times B_{nn} \times Y_{nN}\quad(n\le min\{M,N\})$
直观一点的:

降维表示:
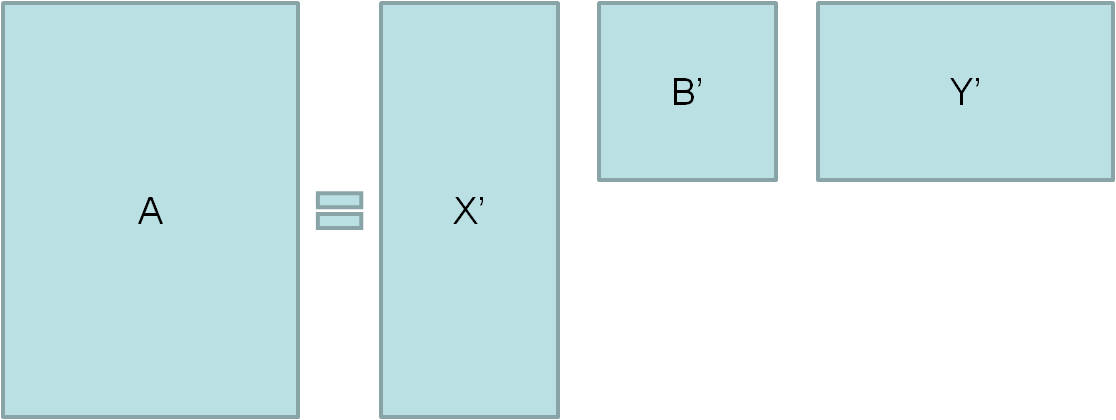
如何从原始的矩阵分解结果得到它的降维表示呢?为什么可以这么做?
由于对角矩阵B的对角线上的元素的很多值相对于其他的值非常小,或者干脆为0,故而可以省略,例如,当B为如下情况时:
$$B_{4 \times 5}=\begin{bmatrix}4 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & \sqrt{5} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}$$
则可以对B进行简化,省略都是0的行和列,得到B’:
$$B’_{3 \times 3}=\begin{bmatrix}4 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & \sqrt{5} \end{bmatrix}$$
那么想对应地,X保留前n列,Y保留前n行
1.2. 如何求出SVD分解后的U,Σ,V这三个矩阵?
对于下面表示形式的奇异值分解
$$A=U \Sigma V^T$$
如果我们将A的转置和A做矩阵乘法,那么会得到n×n的一个方阵$A^TA$。既然$A^TA$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式
$$(A^TA)v_i = \lambda_i v_i$$
这样我们就可以得到矩阵$A^TA$的n个特征值和对应的n个特征向量v了。将ATA的所有特征向量张成一个n×n的矩阵V,就是我们SVD公式里面的$V$矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量
如果我们将A和A的转置做矩阵乘法,那么会得到m×m的一个方阵$AA^T$。既然$AA^T$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
$$(AA^T)u_i = \lambda_i u_i$$
这样我们就可以得到矩阵$AA^T$的m个特征值和对应的m个特征向量u了。将AAT的所有特征向量张成一个m×m的矩阵U,就是我们SVD公式里面的$U$矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量
U和V我们都求出来了,现在就剩下奇异值矩阵$\Sigma$没有求出了
由于$\Sigma$除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值$\sigma$就可以了
由于
$$A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = Av_i / u_i$$
这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵$\Sigma$
那么为什么说$A^TA$的特征向量组成的就是我们SVD中的$V$矩阵,而$AA^T$的特征向量组成的就是我们SVD中的$U$矩阵?
以$V$矩阵的证明为例
$$A=U\Sigma V^T \Rightarrow A^T=V\Sigma^T U^T \Rightarrow A^TA = V\Sigma^T U^TU\Sigma V^T = V\Sigma^2V^T$$
上式证明使用了:$U^TU=I$, $\Sigma^T\Sigma=\Sigma^2$
可以看出$A^TA$的特征向量组成的的确就是我们SVD中的$V$矩阵。类似的方法可以得到$AA^T$的特征向量组成的就是我们SVD中的$U$矩阵
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:
$$\sigma_i = \sqrt{\lambda_i}$$
这样就可以不用 $\sigma_i=Av_i/u_i$ 来计算奇异值,也可以通过求出$A^TA$的特征值取平方根来求奇异值
1.3. SVD的一些性质
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例
也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵
$$A_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n}$$
由于这个重要的性质,SVD可以用于
PCA降维,来做数据压缩和去噪;
推荐算法,将用户和喜好对应的矩阵做特征分解,进而得到隐含的用户需求来做推荐;
NLP中的算法,比如潜在语义索引(LSI)
1.4. 理解SVD分解所得三个矩阵的含义
用一个打矩阵来表示成千上万篇文章和几十上百万个词的关联性
在这个矩阵中,每行表示一个词,每列表示一篇文章,如果有M篇文章,N个词,则可以得到一个MxN的矩阵:
$$
A=
\begin{bmatrix}
a_{11} & a_{12} & … & a_{1M} \\
a_{21} & a_{22} & … & a_{2M} \\
… & … \\
a_{N1} & a_{N2} & … & a_{NM} \\
\end{bmatrix}
$$
其中$a_{ij}$表示的是第j篇文章的第i个词的加权词频(比如用词的TF-IDF)。一般来说这个矩阵会非常非常大
对A进行奇异值分解后:

原始矩阵A的元素个数为$M \times N$,奇异值分解后得到的上小矩阵的元素总是为$M \times n + n \times n + n \times N = n(M+N+n)$,一般情况下$M \times N \gg n(M+N+n)$,这使得数据的存储量和计算量都远小于原始矩阵
这三个矩阵都有非常清晰的物理含义:
矩阵X
矩阵X是对词进行分类的结果,它的每一行表示一个词,每一列表示一个语义相近的词类,或者称为语义类
这一行的每个非零元素表示这个词在每个语义类的重要性(或者说是相关性),例如:
$$X=\begin{bmatrix}0.7 & 0.15 \\ 0.22 & 0.49 \\ 0 & 0.92\end{bmatrix}$$
则第一个词与第一个词类最相关,而与第二个此类的关系比较弱,以此类推
矩阵Y
矩阵Y是对文本的分类结果,它的每一列对应一篇文章,每一行对应一个文章主题
这一列的每个非零元素表示这篇文章在每个的主题重要性(或者说是相关性),例如:
$$Y=\begin{bmatrix}0.7 & 0.15 & 0.22 & 0.39 \\ 0 & 0.92 & 0.08 & 0.53\end{bmatrix}$$
则第一篇文章很明显属于第一个主题,第二篇文章和第二个主题很相关,以此类推
矩阵B
中间的矩阵则表示词的类和文章的类之间的相关性,例如
$$B=\begin{bmatrix}0.7 & 0.21 \\ 0.18 & 0.63 \end{bmatrix}$$
则第一个词的语义类与第一个主题相关,而第二个主题相关性较弱,而第二个词的语义类则相反
1.5. SVD用于PCA降维
用PCA降维,需要找到样本协方差矩阵$X^TX$的最大的d个特征向量,然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出,在这个过程中需要先求出协方差矩阵$X^TX$,当样本数多样本特征数也多的时候,这个计算量是很大的
回顾上面SVD的计算过程,我们可以发现:求$X^TX$的d个最大的特征值对应的特征向量张成的矩阵,其实相当于对$X$进行奇异值分解得到右奇异矩阵$V$
SVD有个好处,有一些SVD的实现算法可以不求先求出协方差矩阵$X^TX$,也能求出我们的右奇异矩$V$。也就是说,我们的PCA算法可以不用做特征分解,而是做SVD来完成,这个方法在样本量很大的时候很有效
实际上,scikit-learn的PCA算法的背后真正的实现就是用的SVD,而不是我们我们认为的暴力特征分解
另一方面,注意到PCA仅仅使用了我们SVD的右奇异矩阵,没有使用左奇异矩阵,那么左奇异矩阵有什么用呢?
假设我们的样本是m×n的矩阵X,如果我们通过SVD找到了矩阵$XX^T$最大的d个特征向量张成的m×d维矩阵$U$,则我们如果进行如下处理:
$$X_{d \times n}’ = U_{d \times m}^TX_{m \times n}$$
可以得到一个d×n的矩阵$X’$,这个矩阵和我们原来的m×n维样本矩阵X相比,行数从m减到了d,可见对行数进行了压缩。也就是说,左奇异矩阵可以用于行数的压缩。相对的,右奇异矩阵可以用于列数即特征维度的压缩,也就是我们的PCA降维。
2. 关键词权重的科学度量TF-IDF
以短语“原子能的应用”为例,可以拆分成三个关键词:“原子能”、“的”和“应用”
主要思想:词出现次数较多的网页应该比它们出现较少的网页相关性高
缺点一:篇幅长度的影响
解决方案:根据篇幅长度,对关键词次数进行归一化,即$TF_c=\frac{n_c}{N}$,称为关键词的“单文本词频” (Term Frequency)
此时,要度量网页与查询之间的相关性,一个简单直接的方法就是:直接使用各个关键词在网页中出现的总词频
若查询包含N个关键词$w_1,w_2,…,w_N$,它们在某个特定网页中的词频分别是$TF_1,TF_2,…,TF_N$,则这个网页的与该查询之间的相关性为:
$$TF_1+TF_2+…+TF_N$$
缺点二:“停止词”的干扰
解决方案:在度量相关性时,不考虑这些词的频率
缺点三:没有考虑不同关键词的信息量。例如,“应用”是个通用的词,而“原子能”是个很专业的词,后者在相关性评估中应该比前者更重要
解决方案:对每个关键词施加一个权重,这个权重的设定必须满足:
预测主题的能力强,则权重大,否则,权重小;
停止词权重为0——不需要对第二个缺点做特殊的处理,在这里就顺带解决了第二个问题;
这样查询与某个网页之间的相关性就变成了:
$$TF_1·IDF_1+TF_2·IDF_2+…+TF_N·IDF_N$$
其中,$IDF_i$是第i个关键词对应的权重
那么具体该如何得到$IDF_i$呢?
基于这样的常识:如果一个关键词只在很少的网页中出现,通过它就容易锁定搜索目标,它的权重就应该大;反之,如果一个词在大量的网页中都出现,看到它仍然难以确定要找什么内容,那么它的权重应该小
因此,假定一个关键词$w$在$D_w$个网页中出现过,那么$D_w$越小,$w$的权重就越大
在信息检索中,使用最多的权重是“逆文本频率指数” (Inverse Document Frequency, IDF)
$$IDF_w=log(\frac{D}{D_w})$$
3. 推荐系统的奥秘
3.1. 基于用户数据:协同过滤算法
归功于亚马逊工程师的“发明”——“一个客户买了这个东西,那么他也可能买另一个东西”
基本思想:
喜好相同的人和人之间有相似的消费/行为模式。喜好这个东西的人,倾向于也喜好另一个
实现的方法为“协同过滤”算法 (collaborative filtering)
下面以音乐推荐系统为例进行说明,基于对用户历史数据的不同侧重,可以分为以下两类应用情景:
(1)基于用户:对每一个用户的听歌偏好作为向量,计算用户喜好之间的相似度,找到与某个用户X喜好最相似的一个其他用户Y,然后将Y的歌单里有而X没有的歌推荐给X
(2)基于项目(单曲):将用户对于一首歌的偏好作为向量,计算单曲之间的相似度,若某个用户喜欢/收藏了某一首歌,则将于这首歌相似的歌曲推荐给这个用户
但是,基于单一协同过滤算法的推荐系统会存在明显的误差:
除了用户及消费模式信息,不涉及被推荐单曲本身的任何信息
这使得热门音乐币冷门音乐更容易得到推荐,因为前者拥有更多数据
如果推荐系统只能给出热门歌曲的推荐,往往很难让人感到惊喜
而基于项目(单曲)的协同过滤,也有一个问题,就是相似使用模式下的内容异质。
例如你听了一张新专辑里面全部的歌,但除了主打歌,其他的一些插曲、翻唱曲以及混音曲可能都不是歌手的典型作品,那么协同过滤在这个时候,就会因为这些「噪音」而产生偏差。
最大的问题便是“没有数据,一切皆失效”
3.2. 基于内容:摆脱协同过滤算法对用户数据的过分依赖
在数据量庞大且足够干净的时候,协同过滤算法是非常强大的,但如果作为一个新用户,在数据稀少的情况下,推荐系统该怎么获知我的口味?
可以利用歌曲本身的信息来得到推荐结果,其基本思想是:
当你喜欢一首歌时,你会倾向也喜欢同类型的其他歌曲
不同歌曲有很多不同的属性,用一个向量去描述该单曲的属性,每一个维度的值代表一个属性的定量描述
按照这些属性,可以计算两首歌曲的相似度
基于内容的推荐算法更像是对协同过滤算法以上缺陷的一种补充——假如没有大量用户数据,或者想听冷门歌曲,我们就只能从音乐本身寻找答案了
前面提到,可以根据歌曲的不同维度的属性去构造一个特征向量去描述它,但是可供选择的属性实在是太多了,因此需要构造的特征向量维度过大——可以利用深度学习建立基于音频的推荐模型,通过特征的embedding和降维方法,把这么多特征映射到低维变量空间里
3.3. 相似度到底是怎么算出来的?
可以拥有描述相似度的统计量为:欧式距离和余弦相似度
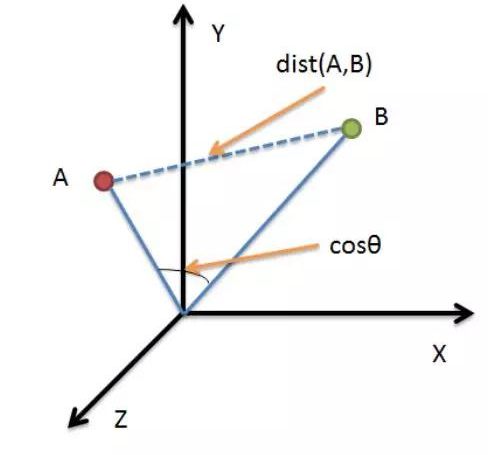
可以看出,在上图中,如果固定B,让A沿着直线OA方向移动,在移动过程中,AB的余弦夹角始终保持不变,而两点之间的绝对距离一直在变化
这种差异使得在使用它们进行相似度描述时,要考虑数据的特性:
(1)欧式距离:能够突出数值绝对差异,在欧式距离下,用户对歌曲的偏好都可以被认为是一样的分数,可以简化歌曲相似度的计算;
(2)余弦相似度:更多是从用户偏好方向上区分差异
4. 用余弦相似度进行文本分类
构造文本特征向量
在 《2. 关键词权重的科学度量TF-IDF》 我们已经讨论过用什么样的特征能够比较好地描述文本的特征信息
因此,这里我们使用TF-IDF来构造文本特征向量:对于一篇文本中的所有实词,计算它们的TF-IDF值
比如,比如词汇表有64000个词,其编号和词如下表所示:
$$\begin{array}{c|c}\hline编号 & 实词 \\ \hline 1 & 阿 \\ 2 & 啊 \\ 3 & 阿斗 \\ … & … \\ \hline \end{array}$$
对于某一篇文本,这64000个词的TF-IDF值如下:
$$\begin{array}{c|c}\hline编号 & TF-IDF \\ \hline 1 & 0 \\ 2 & 0.0034 \\ 3 & 0 \\ … & … \\ \hline \end{array}$$
基于余弦相似度进行文本分类的两种情况
(1)我们已经知道一些新闻类别的特征向量$x_1,x_2,…,x_n$
对任何一个要被分类的文本Y,计算出它与每个特征向量的余弦相似性,基于最近邻算法(Nearest Neighbor)Algorithm),将它归类于于它最相似的那个类别里
(2)事先并不知道这些文本类别的特征向量
可以先采用层次聚类得到模糊的类别标签,至于聚类到什么程度停止,需要根据实际情况人为地控制——这样就得到了一个个小类,可以计算出每个小类的特征向量
这样问题就变成了第一种分类情况了
5. 加密算法
5.1. 对称性加密与非对称性加密
假设一个形象理解的场景:
考试时,超模君通过小天给学渣表妹传递答案
对称性加密

非对称性加密
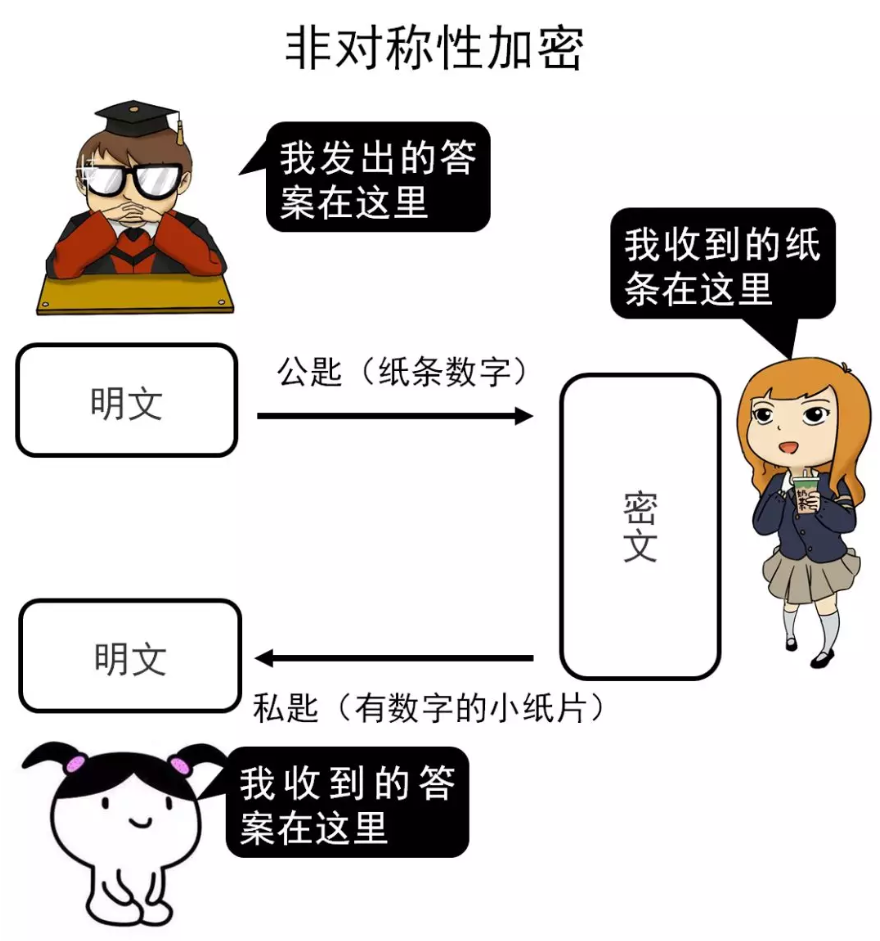
加密和解密规则:
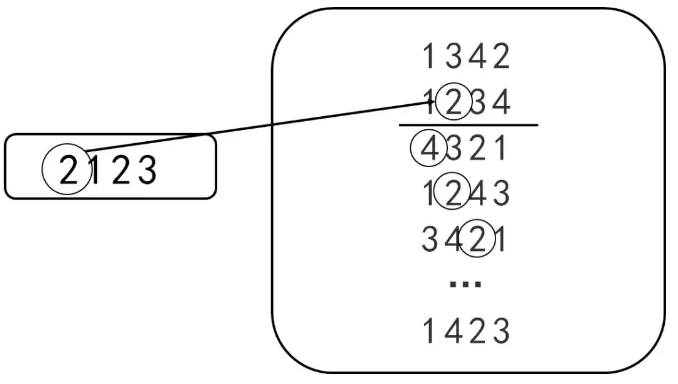
考试前超模君找到表妹,给了她一张纸片,纸片上有20行数,每行有4个数字,4个数字为乱序的1、2、3、4(如下图所示)
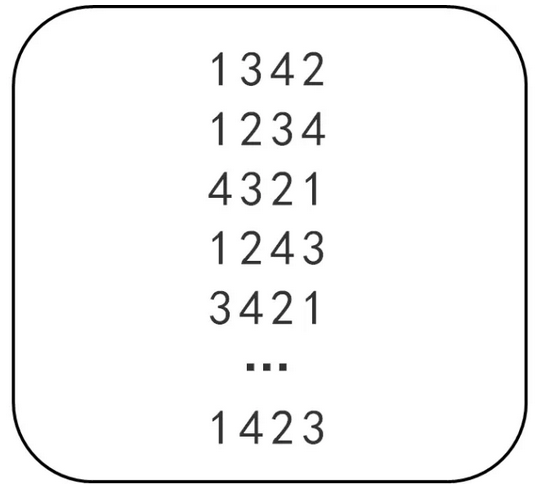
超模君考试时传递的小纸条中第一个数字X1表示纸片中X1行里的第x1个数字,第二个数字X2开始表示下一行中的第X2个数。例如,超模君的纸条上数字为2123,那么根据上面的纸片从第二行开始找数字,得到答案2、4、2、2(下图所示)
非对称性加密与对称性加密最大的区别就在于非对称性加密拥有两把钥匙,分别为私匙和公匙,其中只有公匙会传播出去,而私匙只会在自己手中,不会传播到外界
5.2. RSA加密算法
5.2.1. 加密解密原理
RSA算法是1977年由三位麻省理工学院教授——罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出。RSA就是他们三人姓氏开头字母拼在一起组成的
RSA算法过程:
如何得到公匙$e$和匙$d$
(1) 找出两个质数,一个是$p$,另一个是$q$
(2) 做一个乘法:$n=p\times q$
(3) 取一个函数:$\psi(n)=(p-1)\times(q-1)$
(4) 找出公匙$e$和匙$d$
$$\begin{cases}1<e<\psi(n) \\ e和\psi(n)需要互质 \\ e·d除以\psi(n)余数为1 \end{cases}$$
如何加密和解密
假设传输的信息的数字为$m$,接下来我们就可以得到加密公式:
$$c=m^e \% n$$
其中$\%$为取余运算
c就是我们发送出去的加密后的数字
再来看看解密的公式:
$$m=c^d\%n$$
这个余数就是我们传输的信息——m
举个例子:
(1) 找出两个质数,一个是7,另一个是13
(2) $n=p\times q=7 \times 13=91$
(3) $\psi(n)=(p-1)\times(q-1)=6 \times 12=72$
(4) 找出公匙$e$和匙$d$:$\begin{cases}e=5 \\ d=29\end{cases}$
(5) 假设我们要加密的数字是$m=4$
(6) 加密:$m^e \div n=4^5 \div 91…23$
(7) 解密:$c^d \div n=23^29 \div 91…4$
5.2.2. 安全性分析
为什么RSA算法是安全的(目前来说)?
在传输的过程中,$e$(公匙)、$n$(质数乘积)、$c$(余数)是可以被黑客窃听到的,但参考上面加密公式可以知道 $d$(私匙)和 $\psi(n)$ 没有参与加密过程,所以窃听者并不知道$d$和$\psi(n)$
那么窃听者能不能通过e、n、c算出私匙d呢?
$$
\begin{cases}
(e · d)\,\%\,\psi(n)=1 & (1)\\
\psi(n) = (p-1)(q-1) & (2)\\
n=p·q & (3)
\end{cases}
$$
看看用这3个公式黑客能不能算出私匙d:
假设黑客已经监听到了:
$$e=5,\quad c=23,\quad n=p·q=91$$
根据公式(1)知:
$$5·d\,\%\,\psi(n)=1$$
要想求出$d$就得知道$\psi(n)$,而$\psi(n) = (p-1)(q-1)$
因此要想知道$\psi(n)$,就得知道$p$和$q$,而黑客已经知道了
$$n=p·q=91$$
所以只需要对$n$进行质因式分解,可以得到
$$p=7,\quad q=13$$
从上面的分析中可以看出,破解私匙的关键的一步是对$n$进行因式分解,虽然上面举的例子中的因式分解很简单,分分钟就能被破解,但是在实际使用中的$n$是一个很大的数——1024位的二进制数字,换算成十进制约为308位
目前还没有公式可以对这么大的一个数进行质因式分解,想硬解就需要用穷举法一个个的试出p、q
那么,用普通计算机进行穷举需要花费多久的时间呢?答案是整整一年
6. 信息指纹
任何一段信息(包括文字、语言、视频、图片等),都可以对应一个不太长的随机数,作为区别这段信息和其他信息的指纹
只要算法设计得好,任何段信息的指纹都很难重复
6.1. 应用场景一:爬虫重复项的检查
使用网络爬虫进行网页抓取时,为了防止重复下载同一个网页,需要在散列表中记录访问过的网站 (URL)
但是如果在散列表中以字符串的形式直接存储网址,即小孩内存空间,又浪费查找时间:
现在的网址一般都很长,比如在 百度上查找“吴军 数学之美”,对应的网址长度在100个字符以上
假设网址的平均长度为100个字符,目前互联网上有5000亿这个数量级的网页,那么存储这些网址本身就至少需要50TB。考虑到散列表的存储效率一般在50%左右,所以实际上所需内存在100TB以上
另外。即使这么多的网址放到内存中,由于网址长度不固定,以字符串的形式查找,效率很低
因此,若能找到一个函数,将这5000亿个网址随机映射到128位二进制数上,也就是16个字节的空间,那么内存的需求量就降至原来的 1/6 不到,且这些与网址相对应的指纹长度相同,直接进行整数比较就可以进行快速的查找——空间复杂度和时间复杂度都得到了显著性的降低
6.2. 应用场景二:集合相同的判定
在网页搜索中,有时需要判断两个查询用词是否相同(次序可能不同),比如“北京 中关村 星巴克”和“星巴克 中关村 北京”,它们的用词就完全相同
这其实是一个集合一致性的判断问题
解决这个问题的方法有很多:
(1)笨办法:对集合中的元素一一做比较,时间复杂度为$O(N^2)$
(2)稍微好一些:先排序,然后顺序比较,时间复杂度为$O(N\log N)$
(3)跟(2)效果差不多:将第一个集合放在一个散列里,然后拿第二个集合的元素一一和散列中的元素做比较,时间复杂度为$O(N)$,已经达到最佳,但是额外使用了$O(N)$的空间
最高效的方法是计算这两个集合的指纹,然后直接进行比较
我们定义一个集合$S=\{e_1,e_2,…,e_n\}$的信息指纹为
$$FP(S)=FP(e_1)+FP(e_2)+…+FP(e_n)$$
加法交换律保证了集合的指纹的不因元素出现的次序而改变,如果两个集合的元素相同,则它们的信息指纹也相同——当然可能存在集合不同而指纹相同的情况,但是概率比较小,可以忽略
6.3. 应用场景三:判断集合基本相同
想象一个这样的场景:
一个人用不同的邮箱账号对同一组几乎相同的人群群发垃圾邮件,你现在获得了这两个账户的群发邮件列表,需要根据两个的各种的群发列表来判断它们的一致性,基本相同,则可以做出这样的判断:这两次群发很可能是由同一个人发起的,只是用了不同的邮箱账号而已
那么,如何快速判断两个集合是否基本相同呢?
可以分别从两个账号群发的接收邮箱清单中按照相同的规则随机挑选几个邮箱地址,然后比较它们的指纹,如果它们的指纹相同,则很可能它们的群发邮箱清单基本相同
因为我们比较的是两个集合基本相同,所以有可能抽样构造出来的指纹是不完全一样的,因此需要我们的指纹具有一点的容错能力
这个功能可以引申到另外一个更常见的应用场景——判断一篇文章是否抄袭了另一篇文章
其实这个问题和生物信息学上比较两个基因组(比如人的基因组和猩猩的基因组)是否同源是一个问题
如果把两篇文章从比头到尾(类似于生物信息学上的双序列的全局比对),计算时间太长,也没有必要,因为抄袭的文章一般来说不会完全照搬,而是会在原文的基础上进行语段的顺序的调整(对应到生物学上就是,两个物种有一个相同的祖先,它们都是在祖先基因组的基础上进行基因组重排变异才得到各自现在的基因组),因此若进行全局比对,那么会得出比较大的差异
对于这个问题,我们生物信息学上采用的方法是进行共线性分析:
先找出两个基因组中同源的基因区块(称为block),对应到集合比较问题上,就是把两个集合中的相同/相似元素对应起来;然后再比较两个基因组同源区块在基因组上的排列顺序的一致性,又称为共线性,一般进化距离比较相近的两个物种,比如人和猩猩,它们的基因组间保持了很高的大片段的共线性区域,即共线性保持得很好,而进化距离比较远的两个物种,比如相对于与猩猩,人和老鼠的进化距离就比较远,那么共线性程度肯定没有猩猩的高,因此通过共线性就可以判断出物种在进化上亲缘关系的远近了
对于集合比较问题,在得到原始的对应关系后,不需要像生物学上去比较两个集合元素的排列顺序,只需要比较对应元素的有无即可
因此从生物学上我们得到了启发,最好的做法是:将每一篇文章切成小的片段,假设两篇文章分别拆分出m和n个小片段,然后对这每一个小片段计算它们的指纹,那么原来的两个集合相似性比较的问题,现在变成了$m\times n$个小集合的对应两两比较的问题
只要比较这些指纹,就可以找到大段相同的文字,最后根据时间的先后,判定原创和抄袭
那么如何对每个小片段计算它们的指纹呢?
参考资料:
(1) 吴军《数学之美(第二版)》
(2) 刘建平Pinard《奇异值分解(SVD)原理与在降维中的应用》