1. 最小二乘法
1.1. 最小二乘法与算术平均数
引出问题:
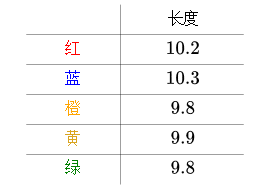
来看一个生活中的例子。比如说,有五把尺子:
用它们来分别测量一线段的长度,得到的数值分别为(颜色指不同的尺子):
之所以出现不同的值可能因为:
- 不同厂家的尺子的生产精度不同
- 尺子材质不同,热胀冷缩不一样
测量的时候心情起伏不定
……
这种情况下,一般取平均值来作为线段的长度:
$$\overline x=\frac 1n \sum_i^n x_i$$
这样做有道理吗?
我们猜测线段的实际长度为X,则任意一个测量值的误差为$|x-x_i|$
由于取绝对值计算起来比较麻烦,大家一般用平方差来表示误差,为$(x-x_i)^2$
则总的误差的平方为:
$$\sum_i^n (x-x_i)^2$$
当猜测的x值取不同的值时,得到的总误差平方会发生改变
而法国数学家,阿德里安-马里·勒让德提出让总误差的平方最小的x就是真值
这就是最小二乘法,即:
$$\epsilon=\sum_i^n (x-x_i)^2 \quad \begin{matrix} \text{最小} \\ \Rightarrow\end{matrix} \quad \text{真值}X$$
那么,在这个规则下,真值X长什么样呢?
这是一个二次函数,对其求导,导数为0的时候取得最小值:
$$\frac{d}{dx}\epsilon = 2 \sum_i^n(x-x_i)$$
令导数为0,则可推出:
$$\sum_i^n(x-x_i)=nx-\sum_i^n x_i=0$$
则
$$x=\frac 1n \sum_i^n x_i$$
正好是算术平均数
1.2. 最小二乘法与正态分布
前面由最小二乘法推出真实值应该是多次测量值的算术平均数
而推导是建立在勒让德的原则正确成立之上的
那么,我们能证明勒让德原则的正确性吗?

数学王子高斯从概率统计角度给出了证明:
每次的测量值$x_i$都和线段长度的真值$x$之间存在一个误差:
$$\epsilon_i=x-x_i$$
这些误差最终会形成一个概率分布,只是现在不知道误差的概率分布是什么,假设概率密度函数为$p(\epsilon)$
再假设一个联合概率密度函数,这样方便把所有的测量数据利用起来:
$$L(x)=p(\epsilon_1)p(\epsilon_2)…p(\epsilon_5)=p(x-x_1)p(x-x_2)…p(x-x_5)$$
因为$L(x)$是关于$x$的函数,并且也是一个概率密度函数
根据极大似然估计的思想,概率最大的最应该出现,当下面这个式子成立时,取得最大值:
$$\frac {d}{dx}L(x)=0$$
假设$p(\epsilon)$满足
$$p(\epsilon)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{\epsilon^2}{2\sigma^2}}$$
即误差的分布是正态分布
此时得出的最大值正好是算术平均数,即$x=\overline x$
2. 为什么正态分布如此常见?

中心极限定理说了,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布,其中有三个要素:
- 独立
- 随机
- 相加
为什么还有很多不是正态分布?
例(1)
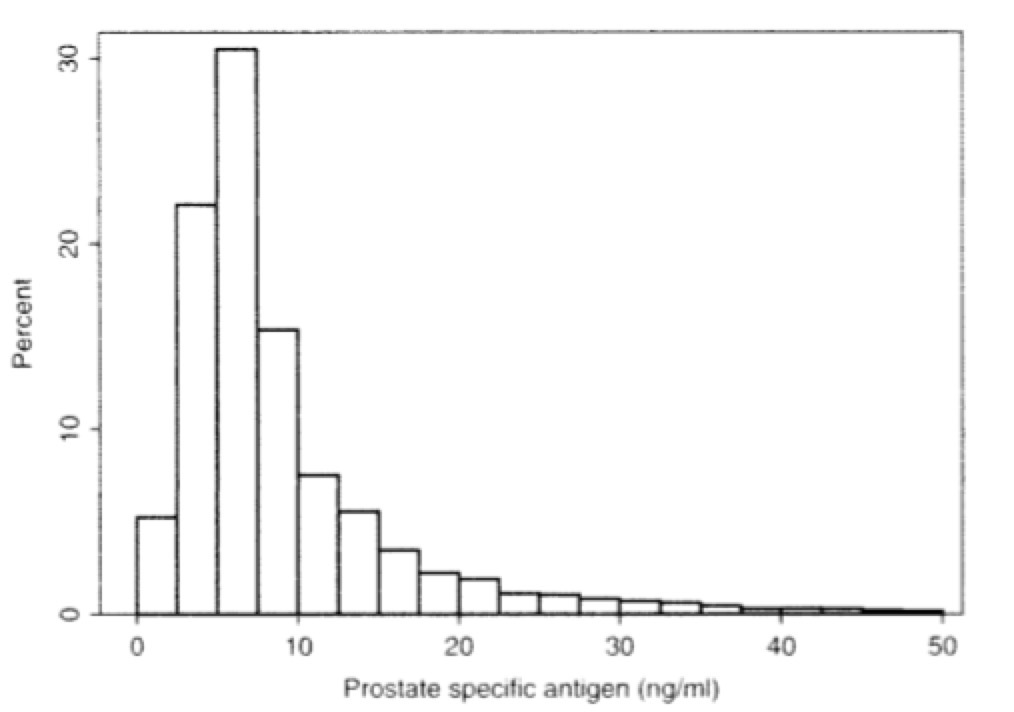
在医学研究中很多分布就不是正态分布,对实施了前列腺癌症治疗的病人进行前列腺特异性抗原(Prostate specific antigen)的检测,检测结果的分布不是正态分布:
这里可能有两个原因导致了这一现象:
样本取自实施了前列腺癌症治疗的病人,这些病人往往有各种各样的疾病,并不是全体人类样本,也就是说不够随机,所以结果很可能会偏向某一边;
癌症并非是相加,癌细胞的分裂更像是乘法;
数学中,可以通过对数来把乘法变为加法:
$$\log(ab)=\log a + \log b$$
因此我们对之前的数据取自然对数,结果就接近于正态分布了(这就是对数正态分布):
<p align=”center
看上去还有点偏向左边,或许是因为采样不是取自全体人类,导致随机性不够
例(2)
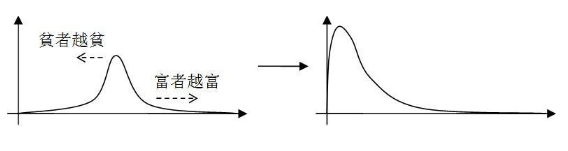
财富分布也是有乘法效应在里面,这就是所谓的“马太效应”:
3. 如何理解协方差、相关系数和点积?
3.1. 欧式距离与余弦距离的点积表示
欧式距离
$\vec a$与$\vec b$的欧氏距离就是下图中的虚线:

欧式距离可以通过勾股定理,或者点积来计算:
$$||\vec a - \vec b||=\sqrt{(a_1-a_2)^2+(b_1-b_2)^2}=\sqrt{(\vec a - \vec b)·(\vec a - \vec b)}$$
余弦距离
$\vec a$与$\vec b$的余弦距离就是下图中$\theta$角的余弦:
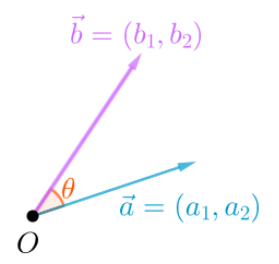
根据线性代数的知识,余弦也可以通过点积和模长来计算:
$$\cos \theta=\frac{\vec a · \vec b}{||\vec a|| · ||\vec b||}$$
3.2. 协方差和相关系数
先假设有两个随机量$X$, $Y$,其均值分别为$\bar{X}$, $\bar{Y}$
由这两个随机量及其均值组成两个向量(可以这么认为,对于随机变量组成的向量,其均值才是原点):
由这两个随机量及其均值组成两个向量(可以这么认为,对于随机变量组成的向量,其均值才是原点):
$$\vec x={X_i - \bar{X}},\quad \vec y={Y_i - \bar{Y}}$$
样本方差
对于$X$,其样本方差为:
$$S_X^2=\frac{1}{n-1}\sum_i^n(X_i-\bar{X})^2$$
通过向量表示为:
$$S_X^2=\frac{\vec x · \vec x}{n-1}$$
方差看起来很像是欧式距离
样本协方差
对于$X$, $Y$,其样本协方差为:
$$S_{XY}=\frac{1}{n-1}\sum_i^n (X_i-\bar{X})(Y_i-\bar{Y})$$
通过向量表示为:
$$S_{XY}=\frac{\vec x · \vec y}{n-1}$$
结合之前的余弦距离的计算公式,我们可以得到:
$$\cos \theta=\frac{\vec x · \vec y}{||\vec x|| · ||\vec y||}=\frac{(n-1)S_{XY}}{||\vec x|| · ||\vec y||}$$
从上面的公式我们可以看出,余弦距离与样本协方差成正比,所以协方差已经可以表示两个向量之间的关系了,但是余弦距离还和两个向量模的乘积成反比,即余弦距离还受到向量长度的影响
样本相关系数
从上面得到的
$$\cos \theta=\frac{\vec x · \vec y}{||\vec x|| · ||\vec y||}=\frac{(n-1)S_{XY}}{||\vec x|| · ||\vec y||}$$
我们可以继续往下推导,得到样本相关系数的计算公式:
$$S_X^2=\frac{\vec x · \vec x}{n-1} \Rightarrow ||\vec x||=\sqrt{n-1}S_X \ S_Y^2=\frac{\vec y · \vec y}{n-1} \Rightarrow ||\vec y||=\sqrt{n-1}S_Y$$
将它们带入上面的式子可以得到:
$$\cos \theta=\frac{(n-1)S_{XY}}{||\vec x|| · ||\vec y||}=\frac{(n-1)S_{XY}}{\sqrt{n-1}S_X · \sqrt{n-1}S_Y}=\frac{S_{XY}}{S_XS_Y}$$
而在课本中给我们的样本相关系数的公式为:
$$r=\frac{S_{XY}}{S_XS_Y}$$
所以说,相关系数其实就是之前说的余弦距离,表示事物之间的相关性
4. 怎样通过抽样数据进行推断才算是“好”?

现实中常常有这样的问题,比如,想知道全体女性的身高均值\mu,但是没有办法把每个女性都进行测量,只有抽样一些女性来估计全体女性的身高
那么根据抽样数据怎么进行推断?什么样的推断方法可以称为“好”?
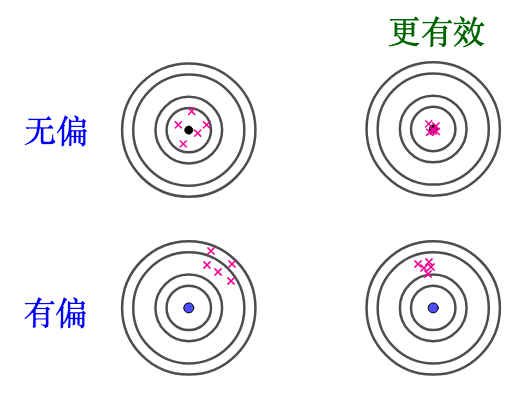
4.1. 无偏性
比如说我们采样到的女性身高分别为:$\{x_1,x_2,…,x_n\}$
那么
$$\overline X = \frac {x_1+x_2+…+x_n}{n}$$
是对$\mu$不错的一个估计,为什么?因为它是无偏估计
由于已知
$$E(X)=\mu$$
可以算出
$$E[\bar{X}]=E\left[\frac {\sum_{i=1}^n X_i}{n}\right]=\frac{E\left[\sum_{i=1}^n X_i\right]}{n}=\frac{\sum_{i=1}^n E[X_i]}{n}=\frac{n\mu}{n}=\mu$$
所以,$\bar{X}$是对$\mu$的无偏估计
但是,如果用以下式子去估计方差$\sigma^2$:
$$S^2=\frac 1n \sum_{i=1}^n (X_i-\bar{X})^2$$
就会产生偏差
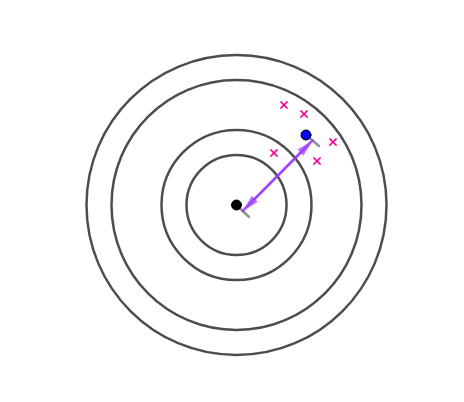
这个偏差经过计算,就是:
$$\frac 1n \sigma^2$$
这种偏差是系统性的
所以这个估计是有偏的
4.2. 有效性
进行估计的时候,估计量越靠近目标,效果越“好”。这个“靠近”可以用方差来衡量
有效估计和无偏估计是不相关的:
举个例子,从$N(\mu,\sigma^2)$中抽出10个样本:
$$\{x_1,x_2,…,x_{10}\}$$
下面两个都是无偏估计量:
$$T_1=\frac{x_1+x_3+2x_{10}}{4} \quad T_2=\frac 1{10} \sum_{i=1}^{10}x_i$$
但是后者比前者方差小,后者更有效
并且在现实中不一定非要选无偏估计量,比如:

4.3. 一致性
如果用以下式子去估计方差$\sigma^2$
$$S^2=\frac 1n \sum_{i=1}^n (X_i - \overline X)^2$$
会有一个偏差:
$$\frac 1n \sigma^2$$
可以看到,随着采样个数n的增加,这个偏差会越来越小。那么这个估计就是“一致”的
如果样本数够多,其实这种有偏但是一致的估计量也是可以选的
5. 为什么样本方差(sample variance)的分母是 n-1?
问题描述:
如果已知随机变量$X$的期望为$\mu$,那么可以如下计算方差$\sigma^2$:
$$\sigma^2=E[(X-\mu)^2]$$
上面的式子需要知道$X$的具体分布是什么(在现实应用中往往不知道准确分布),计算起来也比较复杂
所以实践中常常采样之后,用下面这个$S^2$来近似$\sigma^2$:
$$S^2=\frac 1n \sum_{i=1}^n (X_i-\mu)^2$$
其实现实中,往往连$X$的期望$\mu$也不清楚,只知道样本的均值:
$$\bar{X}=\frac 1n \sum_{i=1}^n X_i$$
那么可以这么来计算$S^2$:
$$S^2=\frac {1}{n-1} \sum_{i=1}^n (X_i-\bar{X})^2$$
那么,这里就引出了两个问题:
为什么可以用$S^2$来近似$\sigma^2$?
为什么使用$\overline{X}$替代$\mu$之后,分母是$\displaystyle\frac{1}{n-1}$?
5.1. 为什么可以用$S^2$来近似$\sigma^2$?
举个例子,假设$X$服从这么一个正态分布:
$$X \sim N(144,1.4^2)$$
即,$\mu=145$,$\sigma^2=1.4^2=1.96$,图形如下:

当然,现实中往往并不清楚$X$服从的分布是什么,具体参数又是什么?所以我用虚线来表明我们并不是真正知道$X$的分布:

很幸运的,我们知道$\mu=145$,因此对$X$采样,并通过:
$$S^2=\frac 1n \sum_{i=1}^n (X_i-\mu)^2$$
来估计$\sigma^2$
某次采样计算出来的$S^2$:

看起来比$\sigma^2=1.96$要小。采样具有随机性,我们多采样几次,$S^2$会围绕$\sigma^2$上下波动——这种偏差是随机的
在这种情况下,可以算出
$$
\begin{aligned}
&\quad E\left[\frac 1n \sum_{i=1}^n (X_i-\mu)^2\right]\\
&= \frac {E\left[\sum_{i=1}^n (X_i-\mu)^2 \right]}{n} \\
&= \frac {\sum_{i=1}^n E[(X_i-\mu)^2]}{n} \\
&= \frac{\sum_{i=1}^n \text{Var}[X_i]}{n} \\
&= \frac{n\sigma^2}{n} \\
&= \sigma^2
\end{aligned}
$$
所以用$S^2$作为$\sigma^2$的一个无偏估计量,算是可以接受的选择
5.2. 为什么使用$\overline{X}$替代$\mu$之后,分母是$\displaystyle\frac{1}{n-1}$?
更多的情况,我们不知道$\mu$是多少的,只能计算出$\overline{X}$。不同的采样对应不同的$\overline{X}$
对于某次采样而言,它的采用$\{x_1,x_2,…,x_n\}$是确定的,则$\overline X$也是固定的,而我们不知道实际的$\mu$是多少,我们考虑实际的$\mu$的所有可能取值,发现对于下面的式子:
$$\sum_{i=1}^n (X_i-\mu)^2$$
当$\mu=\overline{X}$时,其取到最小值

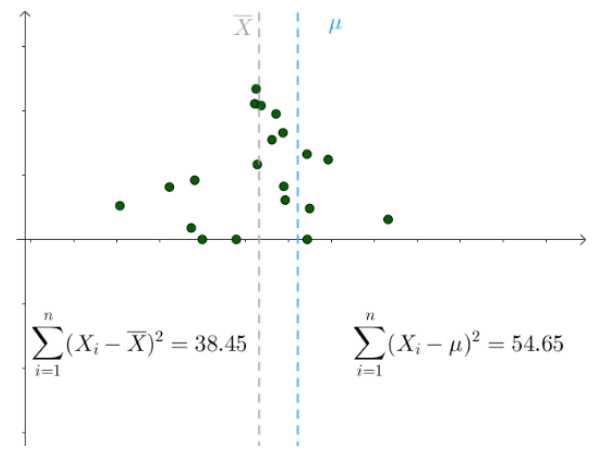
所以可知:
$$\sum_{i=1}^n (X_i-\overline{X})^2 \le \sum_{i=1}^n (X_i-\mu)^2$$
可推出:
$$\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2 \le \frac 1n \sum_{i=1}^n (X_i-\mu)^2$$
进而推出:
$$E\left[\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2\right] \le \left[\frac 1n \sum_{i=1}^n (X_i-\mu)^2\right] = \sigma^2$$
也就是说,如果用$\displaystyle S^2=\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2$去估计$\sigma^2$,总会倾向于低估$\sigma^2$,所以这种估计是存在系统偏差的
那么,具体小了多少,我们可以来算下:
$$
\begin{aligned}
&\quad E[S^2] \\
&= E\left[\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2\right] \\
&= E\left[\frac 1n \sum_{i=1}^n [(X_i-\mu)-(\overline{X}-\mu)]^2\right] \\
&= E\left[ \frac 1n \sum_{i=1}^n \left((X_i-\mu)^2 - 2(X_i-\mu)(\overline{X}-\mu) + (\overline{X}-\mu)^2 \right) \right] \\
&= E\left[ \left(\frac 1n \sum_{i=1}^n (X_i-\mu)^2\right) -\left(\frac 2n (\overline{X}-\mu)\sum_{i=1}^n (X_i-\mu) \right) + \left((\overline{X}-\mu)^2 \right) \right] \\
&= E\left[ \left(\frac 1n \sum_{i=1}^n (X_i-\mu)^2\right) - \left(\frac 2n (\overline{X}-\mu)n(\overline{X}-\mu) \right) + \left((\overline{X}-\mu)^2 \right) \right] \\
&= E\left[ \left(\frac 1n \sum_{i=1}^n (X_i-\mu)^2\right) - \left((\overline{X}-\mu)^2 \right) \right] \\
&= \sigma^2 - E\left[(\overline{X}-\mu)^2 \right]
\end{aligned}
$$
其中,
$$E\left[(\overline{X}-\mu)^2 \right] = \frac 1n \sigma^2$$
下面给出推导:
$$\begin{aligned} &\quad E\left[(\overline{X}-\mu)^2 \right] \\ &= E\left[(\overline{X}-E[\overline X])^2 \right] \\ &= \text{Var}(\overline X) \\ &= \text{Var}\left(\frac{\sum_{i=1}^n X_i}{n}\right) \\ &= \frac{1}{n^2} \text{Var}\left( \sum_{i=1}^n X_i\right) \\ &= \frac{1}{n^2} \sum_{i=1}^n \text{Var} (X_i) \\ &= \frac{n\sigma^2}{n^2} \\ &= \frac 1n \sigma^2 \end{aligned}$$
所以:
$$E\left[\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2\right]= \sigma^2 - \frac 1n \sigma^2 = \frac {n-1}{n} \sigma^2$$
因此
$$
\begin{aligned}
&\quad \sigma^2 \\
&= \frac {n}{n-1} E\left[\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2\right] \\
&= E\left[ \frac {n}{n-1}\frac 1n \sum_{i=1}^n (X_i-\overline{X})^2\right] \\
&= E\left[ \frac {1}{n-1} \sum_{i=1}^n (X_i-\overline{X})^2\right]
\end{aligned}
$$
因此使用下面这个式子进行估计,得到的就是无偏估计:
$$S^2=\frac {1}{n-1} \sum_{i=1}^n (X_i-\overline{X})^2$$
参考资料:
(1) 如何理解最小二乘法?
(2) 为什么正态分布如此常见?
(3) 如何理解协方差、相关系数和点积?
(4) 如何理解无偏估计量?