1. 传统神经网络架构及其存在的问题
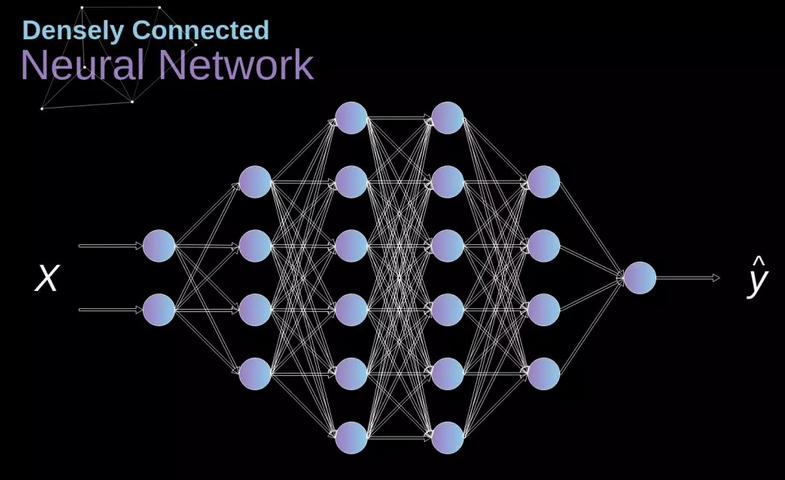
当我们基于一个有限的固定特征集合解决分类问题的时候,上图这种传统架构的神经网络是奏效的
但是当处理照片的时候,问题变得更加复杂:
最简单的做法是,我们把每个像素的亮度视作一个单独的特征,然后将它作为密集网络的输入传递进去
如果我们这么做,为了让它能够应付一张典型的智能手机照片,我们的网络必须包含数千万甚至上亿的神经元(尤其是神经网络的输入层的神经元数量庞大),神经网络越庞大意味着计算和存储开销就越大,别说是普通智能手机了,就是高配的PC机也hold不住
为了减小计算和存储开销,可以将照片缩小,但是我们也会在这个过程中损失有价值的信息
有没有一种方法可以在用神经网络处理图像数据时,既能尽可能多的利用数据,同时还能减少必需的计算量和参数
这就是CNN了
2. 数字照片的数据结构
图像实际上就是巨大的数字矩阵,每个数字代表的是一个单独像素的亮度
在 RGB 模型中,彩色图片是由 3 个这样的矩阵组成的,每个矩阵对应着 3 个颜色通道(红、绿、蓝)中的一个,在黑白图像(专业说法为灰度模式)中,我们仅使用一个矩阵
每个矩阵都存储着 0 到 255 的数值。这个数值范围是图像存储信息的效率(256 个数值刚好对应一个字节)和人眼敏感度之间的折中(我们仅能区分同种颜色的几种有限色度)

3. 卷积
3.1. 什么是卷积?
我们有一个小的数字矩阵(称作卷积核或滤波器),我们将它传递到我们的图像上,然后基于滤波器的数值进行变换,后续的特征图的值要通过下面的公式计算:
$$G(m,n)=(f*h)[m,n]=\sum_j\sum_k h(j,k)f(m-j,n-k)$$
其中输入图像被记作 f,我们的卷积核为 h,计算结果的行列索引分别记为 m 和 n
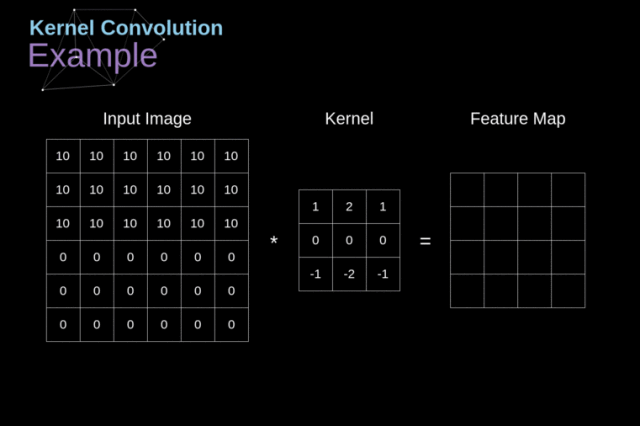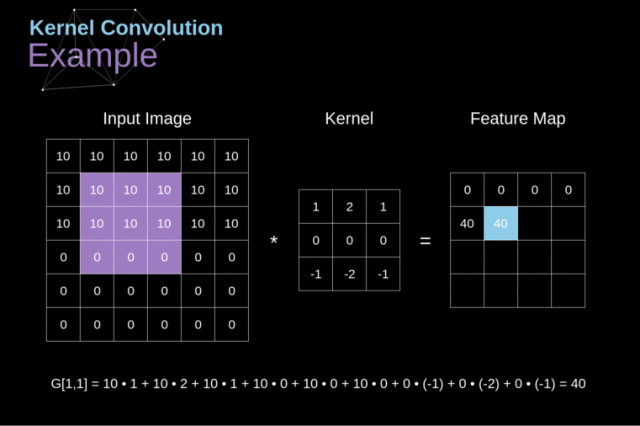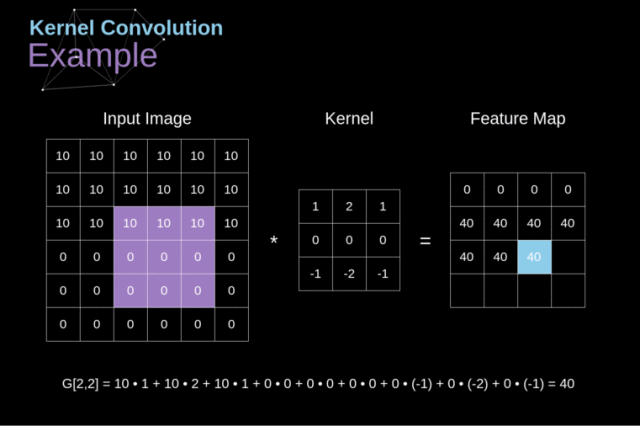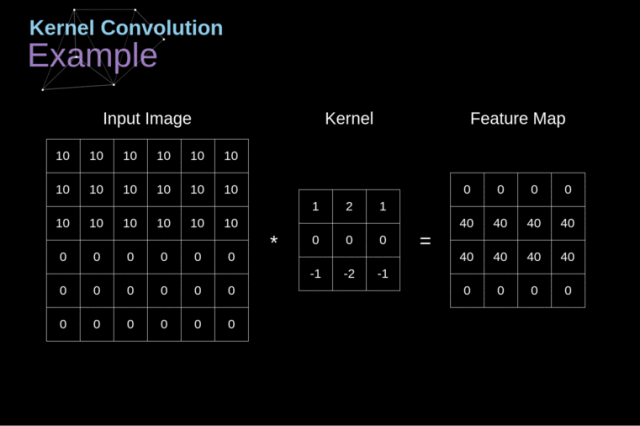
简单来说,就是将我们的滤波器放在选中的像素上之后,将卷积核中的每一个数值和图像中对应的数值成对相乘。最后将乘积的结果相加,然后把结果放在输出特征图的正确位置上
我们来看看在整张图上执行卷积运算之后得到的结果:

用卷积核寻找边缘
3.2. 主要的卷积类型
3.2.1. Valid 和 Same 的卷积
当我们在用 3x3 的卷积核在 6x6 的图像上执行卷积时,我们得到了 4x4 的特征图,即图像的尺寸在每次卷积的时候都会收缩,在图像完全消失之前,我们只能做有限次的卷积
注意一下卷积核是如何在图像上移动的,我们会发现,边缘的像素会比中央的像素影响更小,这样的话我们会损失图片中包含的一些信息
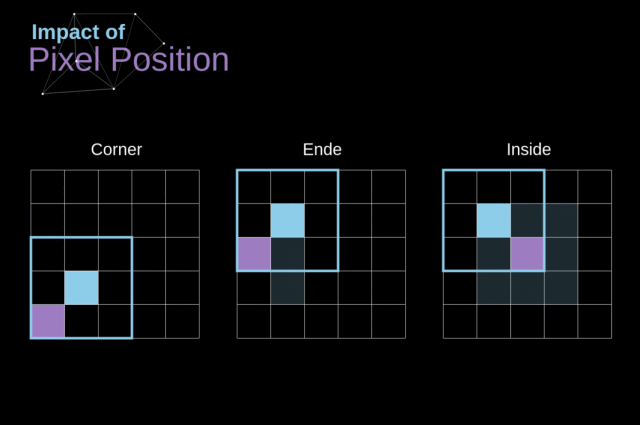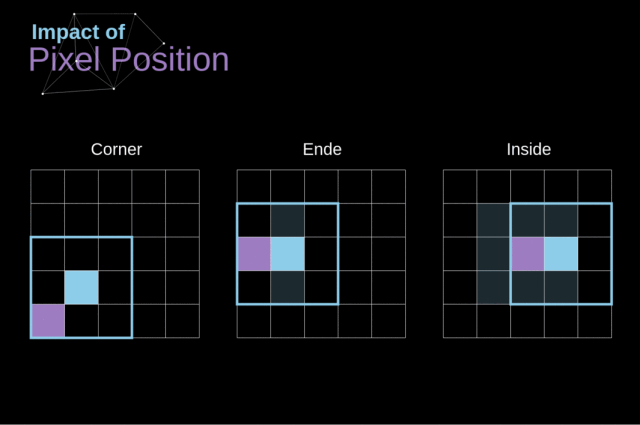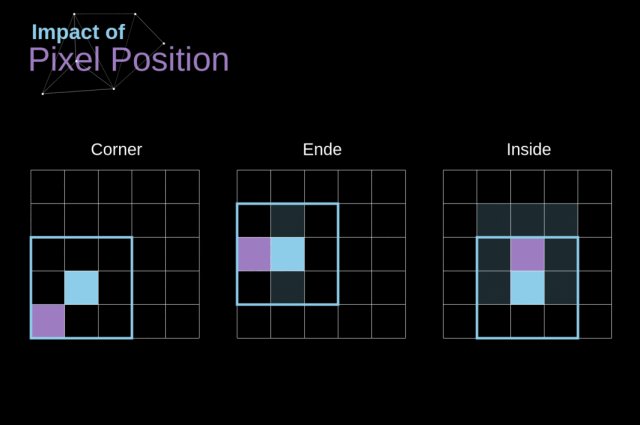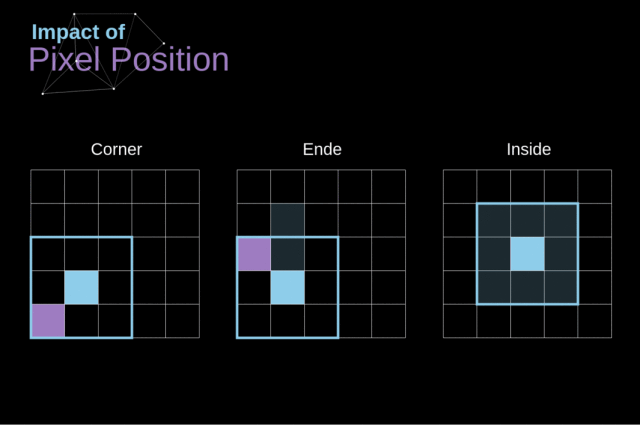
为了解决这两个问题,我们可以使用一个额外的边界来填充图像
例如,如果我们使用 1 像素的填充,我们将图像的尺寸增大到了 8x8,这样,3x3 的滤波器的输出将会成为 6x6。通常在实际中我们用 0 来做额外的填充
根据我们是否使用填充,我们会进行两种类型的卷积:
Valid:代表我们使用的是原始图像;
Same:代表我们在图像周围使用了边界,因此输入和输出的图像大小相同;
对于 Same 卷积,扩充的宽度应该满足下面的方程:
$$p=\frac{f-1}{2}$$
其中 p 是 padding(填充),f 是滤波器的维度(通常是奇数)
3.2.2. 跨步卷积
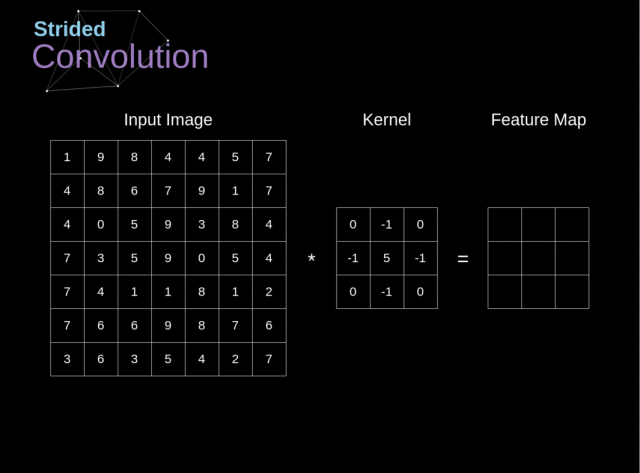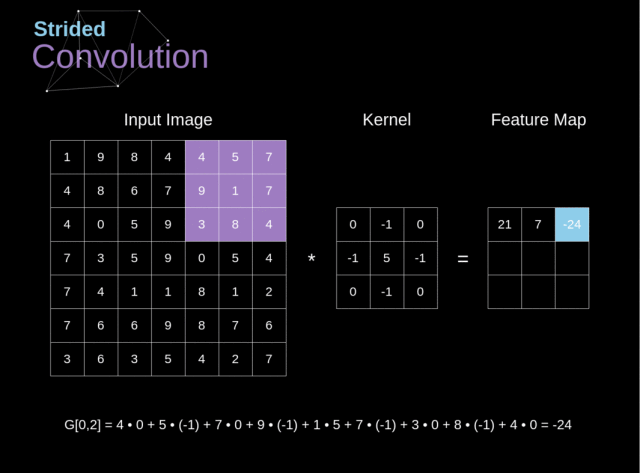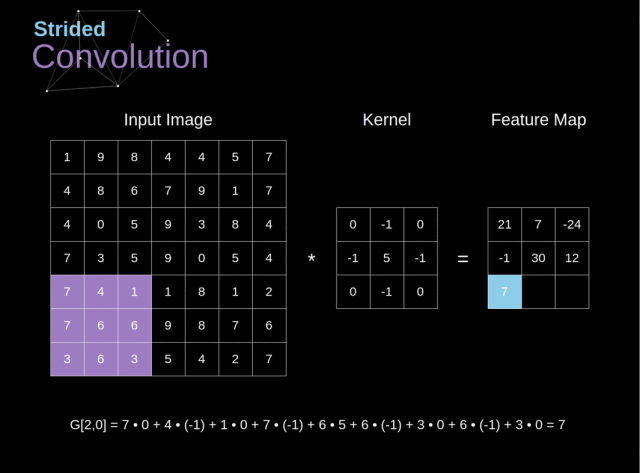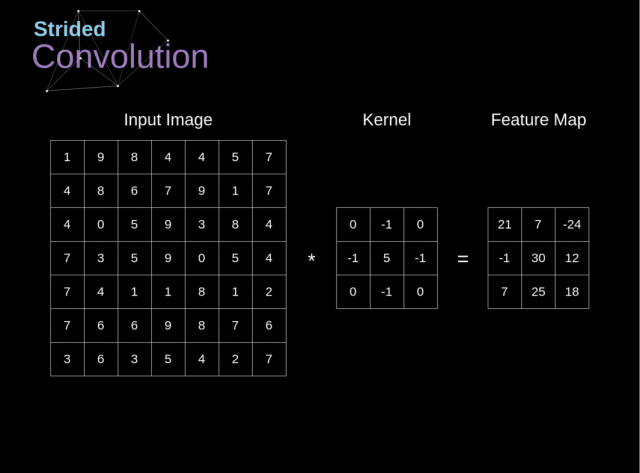
在之前的例子中,我们总是将卷积核移动一个像素。但是,步长也可以看做是卷积层的一个参数
在设计 CNN 结构时,如果我们想让接受域有更少的重叠或者想让特征图有更小的空间维度,那么我们可以决定增大步长
考虑到扩充和跨步,输出矩阵的维度可以使用下面的公式计算:
$$n_{out}=\left\lfloor \frac{n_{in}+2p-f}{s}+1\right\rfloor$$
3.2.3. 立体卷积
立体卷积是一个非常重要的概念,它不仅让我们能够处理彩色图像,而且更重要的是,可以在一个单独的层上使用多个滤波器
最重要的规则是,滤波器和你想在其上应用滤波器的图像必须拥有相同的通道数
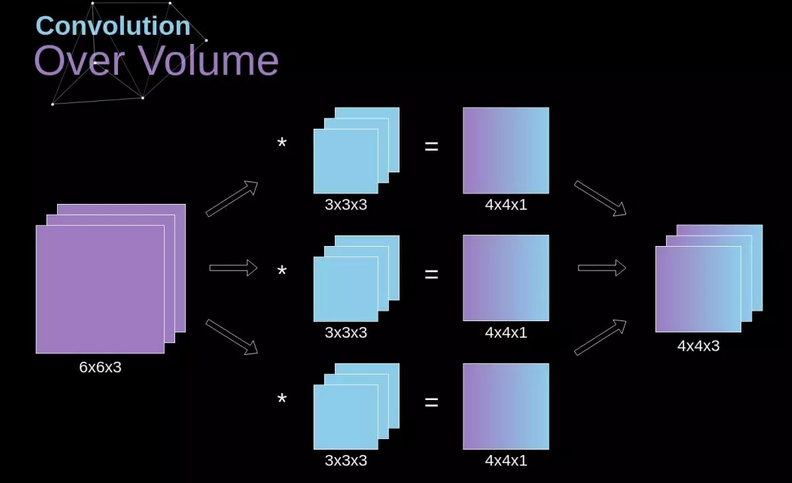
如果我们想在同一张图像上应用多个滤波器,我们会为每个滤波器独立地计算卷积,然后将计算结果逐个堆叠,最后将他们组合成一个整体,得到的张量(3D 矩阵可以被称作张量)
3.2.4. 卷积层
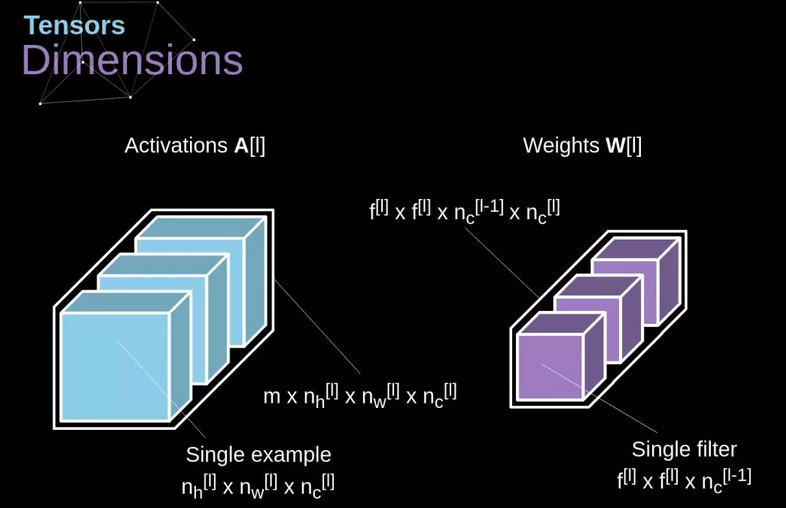
前向传播包含两个步骤:
(1)计算中间结果 Z,它是由前一层的输入数据与张量 W(包含滤波器)的卷积结果,加上偏置项 b 得到的
$$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$$
(2)给我们的中间结果应用一个非线性的激活函数(我们的激活函数记作 g)
$$A^{[l]}=g^{[l]}(Z^{[l]})$$
3.3. 卷积是如何优化计算的?
通过将卷积层与全连接层的比较,就可以看出里面的原因了
在下图中,2D 卷积以一种稍微不同的方式进行了可视化——用数字 1-9 标记的神经元组成接收后续像素亮度的输入层,A-D 这 4 个单元代表的是计算得到的特征图元素
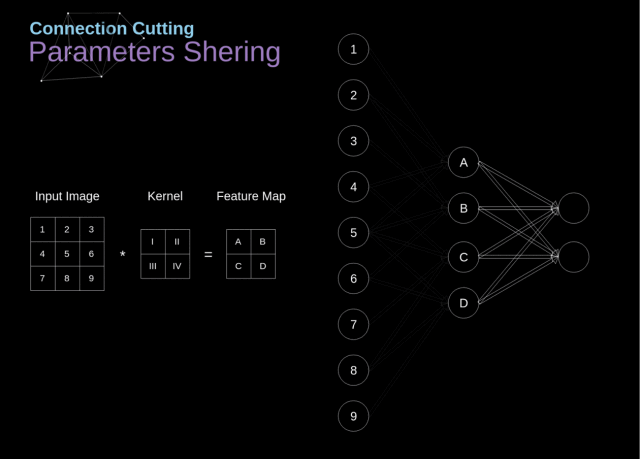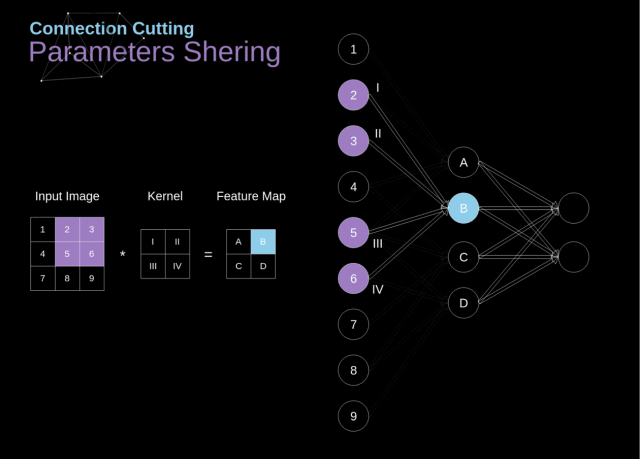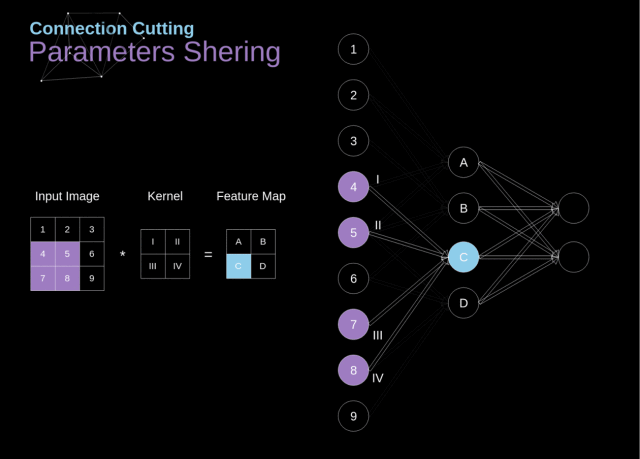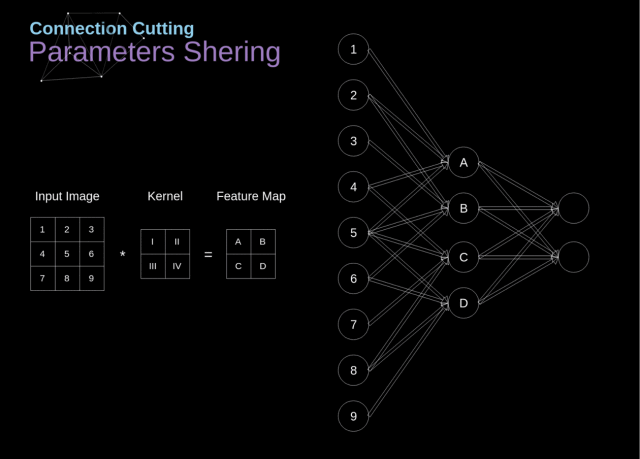
从上图我们可以看出卷积层的两个重要属性:
在前两层中,并不是所有的神经元都是彼此相连的。例如,单元 1 仅仅会影响到 A 的值;
一些神经元会共享相同的权重;
这两个属性都意味着我们要学习的参数数量要少很多
3.4. 卷积层反向传播
在CNN中反向传播包括两部分:
全连接层的反向传播,这个传播过程在全连接网络部分讨论过,这里不再进行说明;
卷积层的反向传播,在前面讨论卷积是如何实现优化计算的问题中,我们将卷积层与全连接层进行了比较,发现了卷积层连接形式的两个重要属性,因此梯度在卷积层的反向传播形式和全连接层是不同的;
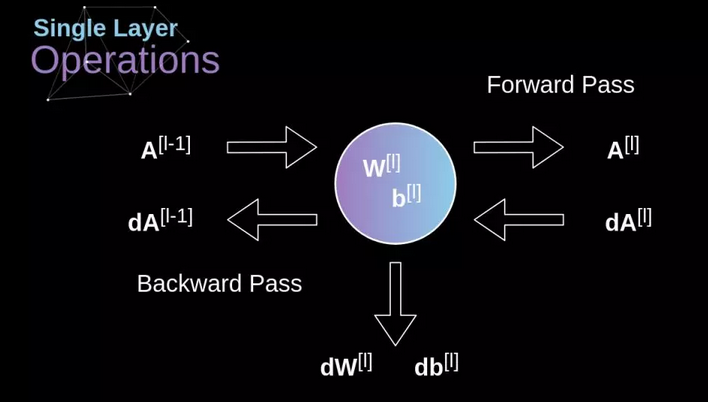
我们的任务是计算 $dW^{[l]}$ 和 $db^{[l]}$——它们是与当前层的参数相关的导数,还要计算 $dA^{[l-1]}$,它们会被传递到之前的层
(1)通过在我们的输入张量上应用我们的激活函数的导数,得到中间值 $dZ^{[l]}$
$$dZ^{[l]}=dA^{[l]}g^{‘[l]}(Z^{[l]})$$
(2)处理卷积神经网络自身的反向传播
为了达到这个目的,我们会使用一个叫做全卷积的矩阵运算——见下图
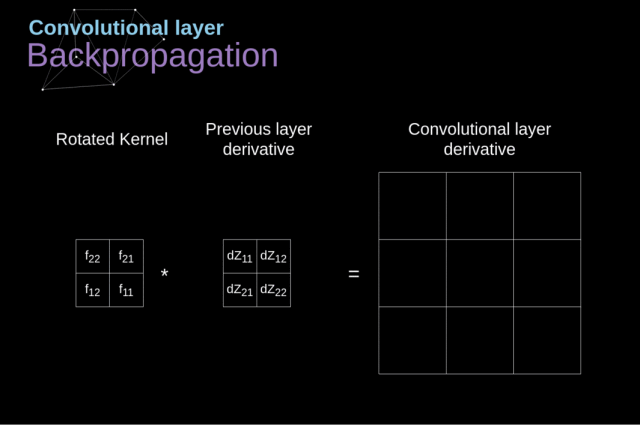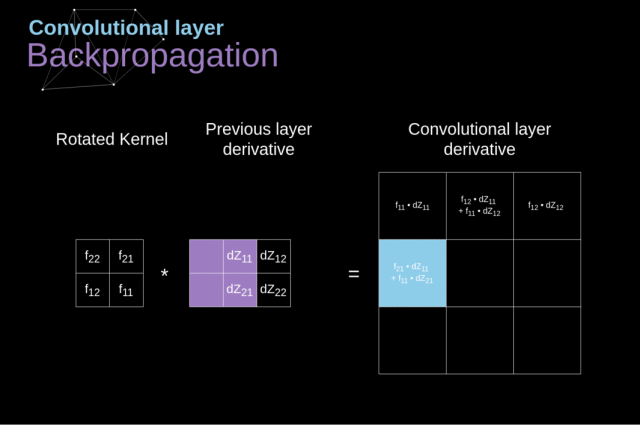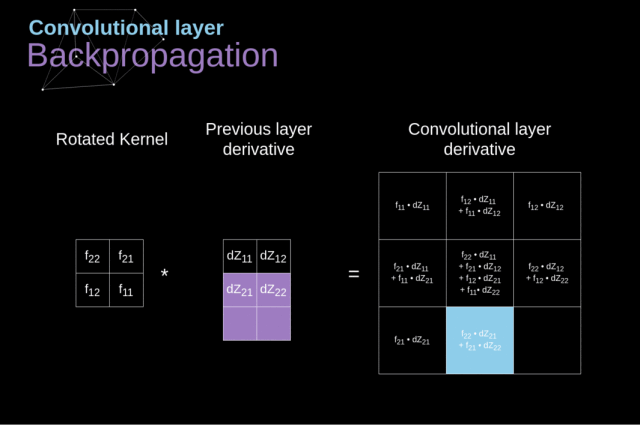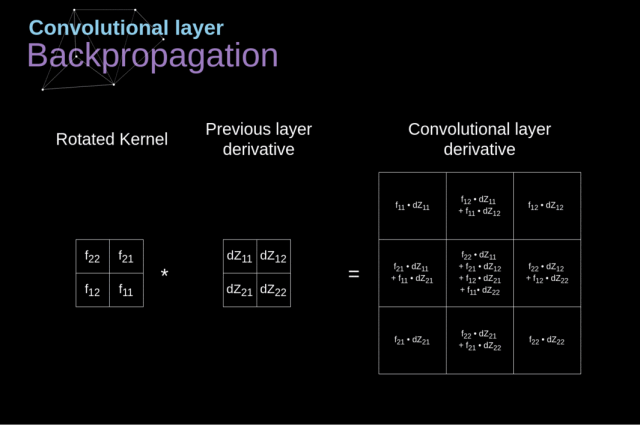
4. 池化层
4.1. 什么是池化?
池化层最早被用来减小张量的大小以及加速运算
池化层的运算比较简单:将我们的图像分成不同的区域,然后在每一个部分上执行一些运算
例如,如下图,对 Max Pool 层而言,我们会选择每个区域的最大值,并将它放到对应的输出区域
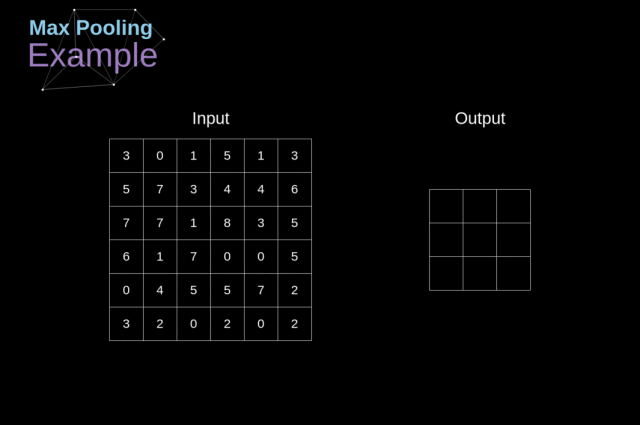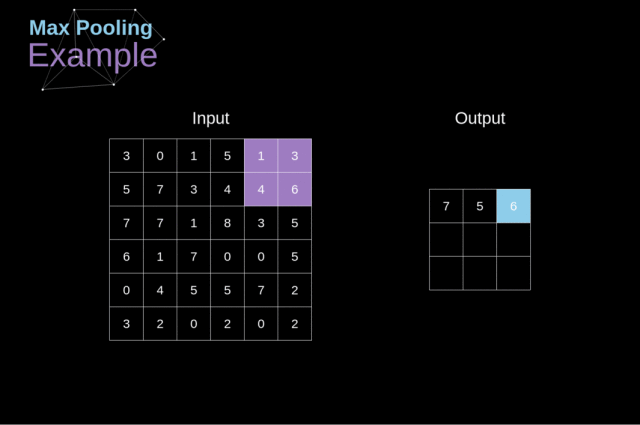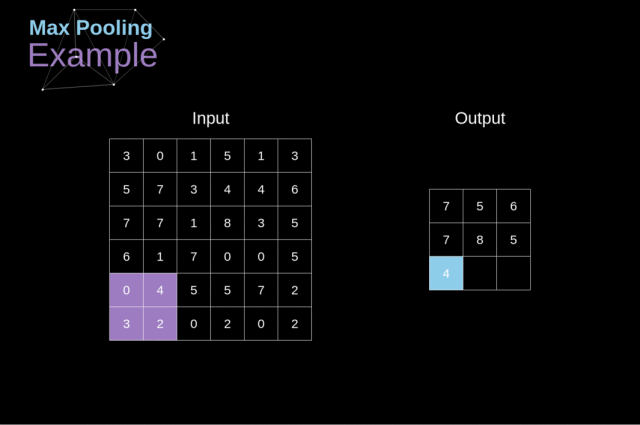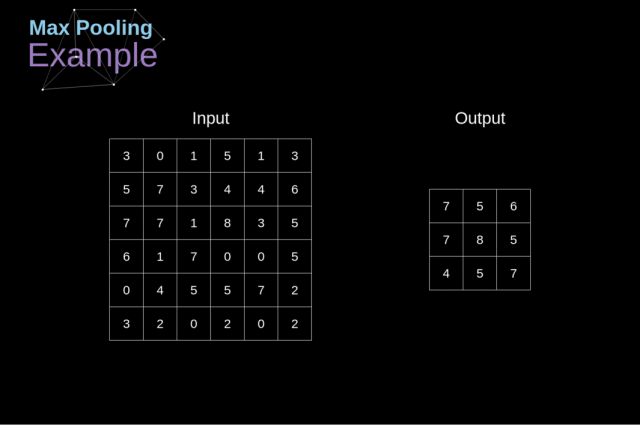
与卷积层的情况一样,我们有两个可用的超参数——滤波器大小和步长
最后但同样重要的一点是,如果你对一个多通道的图像执行池化操作,那么每一个通道的池化应该单独完成
4.2. 池化层反向传播
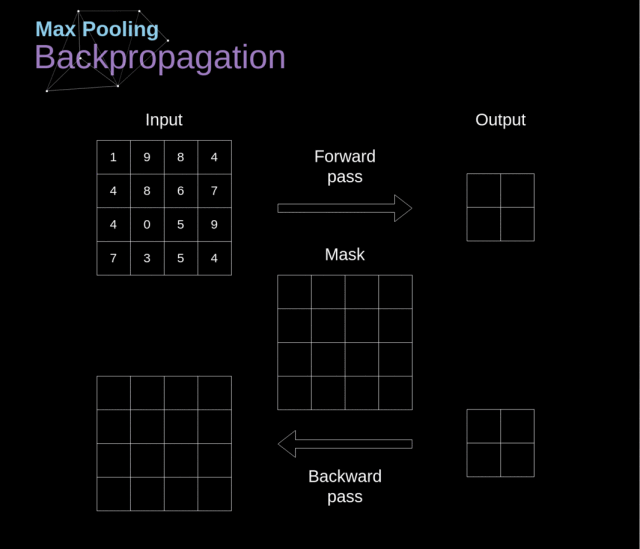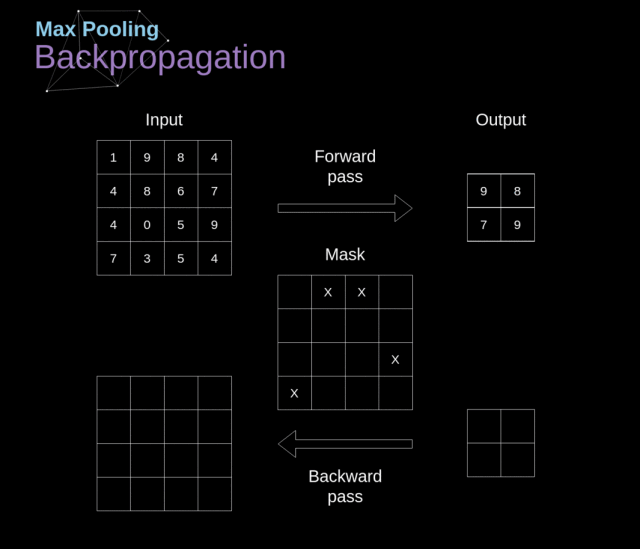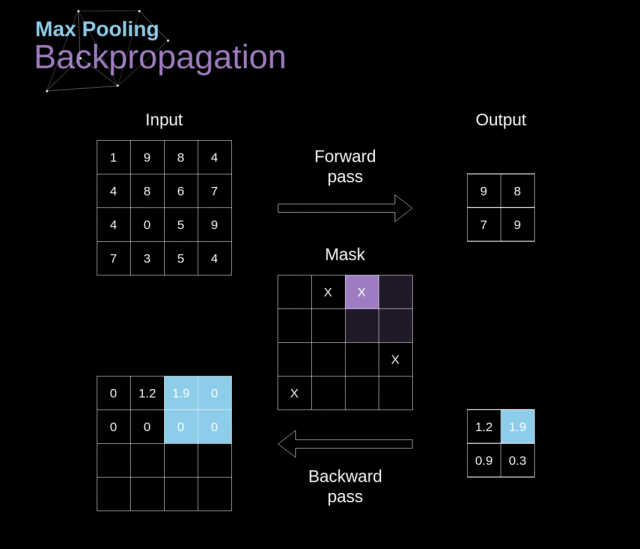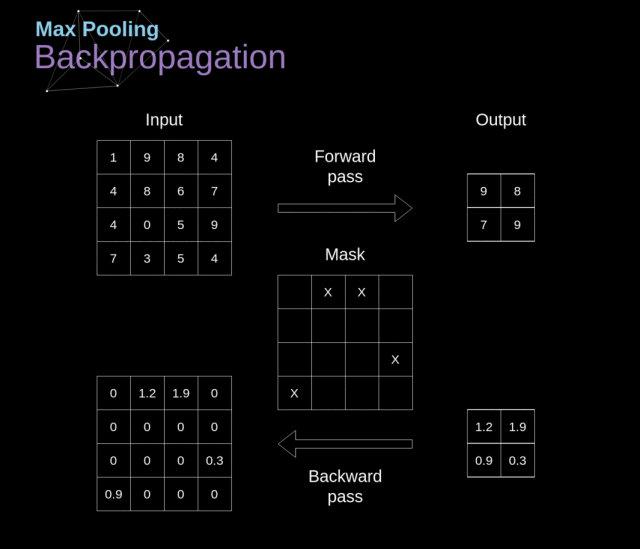
我们在这篇文章中只讨论最大池化反向传播,但是我们学到的规则是适用于所有类型的池化层的——只需要做微小的调整即可:因为在这种层中,我们没有任何必须更新的参数,所以我们的任务就是合适地分配梯度
在最大池化的前向传播中,我们选择的是每个区域的最大值,并将它传递到了下一层。所以在反向传播中也是很清晰的,梯度不应该影响前向传播中不包含的矩阵的元素。实际上,这是通过创建一个掩膜来完成的,这个掩膜记住了前一阶段数值的位置,我们可以在后面转移梯度的时候用到
补充知识
参考资料: